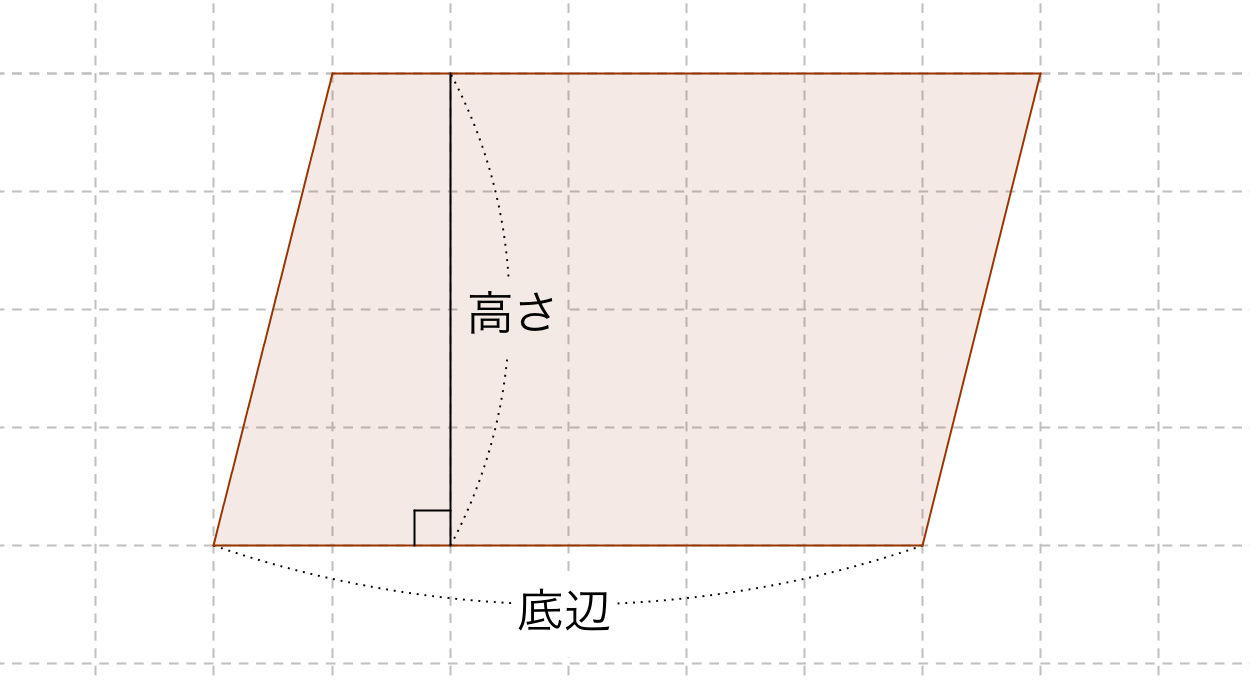
平行四辺形は2つの 合同 な 三角形 を2つ、対応するひと組の辺を共有し、その両端の頂点が対応と逆順に重なるように並べた図形である。 三角形の面積を 〔底辺〕×〔高さ〕÷2 で表すことができるのは、それが平行四辺形の面積を2等分して求めた結果だなぜ? 平行四辺形の面積が \( 底辺 \times 高さ \) となるのかを考えてみましょう。 図のように垂線を引き、平行四辺形を「赤い部分」と「青い部分」に分けます。 「青い部分」を切り取って、「赤い部分」の左側へ移動すると、このように平行四辺形は「長方形」に変形できることがわかり1平行四辺形とは? 平行四辺形は、向かい合う2組の辺が平行な四角形です。 ある四角形について,①2組の対辺がそれぞれ平行であると示せば,平行四辺形であることが証明できるのはわかりますね。 2ポイント ただし,「2組の対辺が平行=平行四辺形」と覚えるだけでは,平行四辺形の
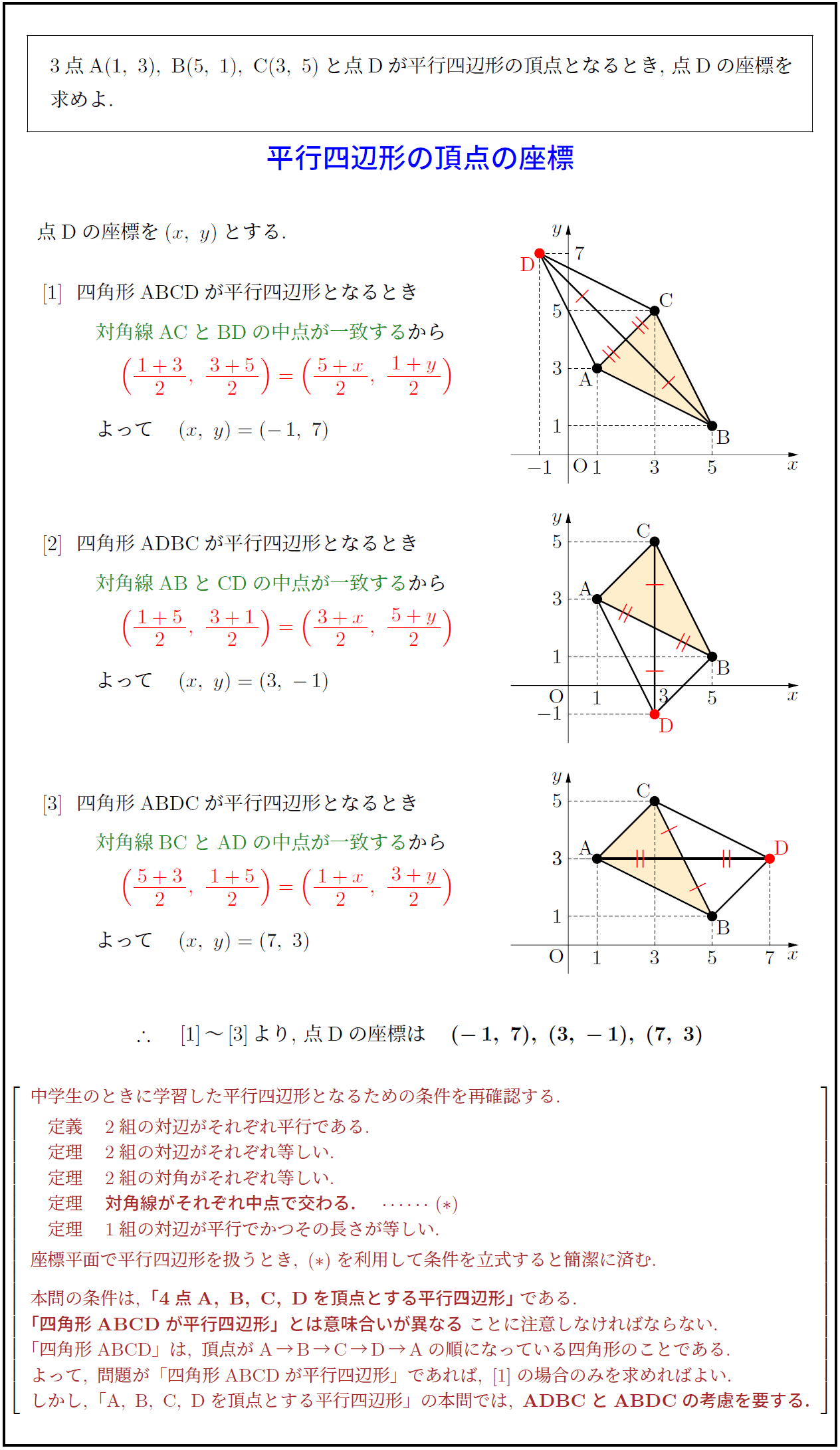
高校数学 平行四辺形の頂点の座標 受験の月
平行四辺形の定義
平行四辺形の定義-ブリタニカ国際大百科事典 小項目事典 平行四辺形の用語解説 2組の対辺がともに平行である四角形。次のような性質をもつ。(1) 2組の対辺の長さはそれぞれ等しい。(2) 2組の対角の大きさはそれぞれ等しい。(3) 2本の対角線はそれぞれの中点で交わる。1組の対辺が平行な四角形は台形なので平行四辺形から これら、対角線をはさむ二つの平行四辺形を 除いて残る 二つの平行四辺形をいう。 (以下、定義の補足(命題1-43)(対角線をはさむ平行四辺形・補形)という。) 命題1-44作図線分,三角形,直線角と平行四辺形)
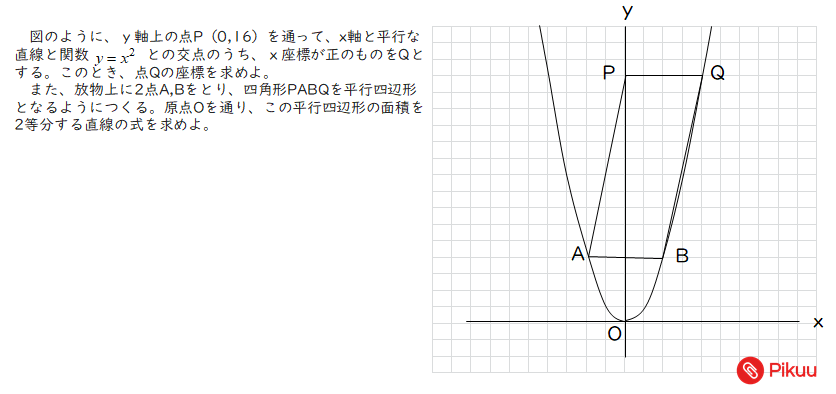



中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu
平行四辺形 ひし形 台形 年 組 名前 3定 じょう ぎや分度器ではからずに、平行四辺形の辺の長さや角度を求 もと めましょう。 2平行四辺形をかきましょう。 ①平行な直線を使って、平行四辺形を かきましょう。 例 れい ② 方がん(ます)を使って、平行四平行四辺形の定義とは まず、「平行四辺形とは何か」口で説明できるでしょうか。 しっかり定義を押さえておきましょう。 平行四辺形2組の対辺がそれぞれ平行である四角形のこと。 図で表すとこうなります↓↓↓ ただ、ここからわかることはこれだけご覧いただきありがとうございます。以下、目次です127 三角形の面積の求め方 復習350 三角形の面積の求め方 参考522 問題の解き方(直線jkは辺ab
平行四辺形の性質 中2数学 平行四辺形の性質はたくさんあります。 それにより、平行四辺形はテストや入試でとてもよく出てくる図形です。 その性質をこのプリントで練習して理解してくださいね。 平行四辺形の2つの角度がわかったね。 つぎは、 残り2つの角度をたしたらいくつになる?? ってことを計算するよ。 四角形の内角の和は、 360° だったよね?? この「360°」から2つの角度をひけばいいんだ。 平行四辺形abcdでいうと、平行四辺形 出典 フリー多機能辞典『ウィクショナリー日本語版(Wiktionary)』 ナビゲーションに移動 検索に移動 ウィキペディアに「平行四辺形」の記事があります。 目次 1 日本語 11 名詞 111 発音 (?) 112 関連語;
平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の面積sは 〔底辺〕×〔高さ〕 で求めることができる。これは平行四辺形を面積を変えずに長方形に変形させることで説明できる 。「平行四辺形の証明」について詳しく知りたい方はこちら 3 平行四辺形に条件をプラスする問題 問題1 平行四辺形abcdの対角線の交点をoとする。次の①~⑤の条件を加えると,平行四辺形abcdはどのような四角形になるか,答えなさい。日本語 名詞 平 行 四 辺 形(へいこうしへんけい) 二組の




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
平行四辺形になる条件 四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。(定義) 2 2組の向かいあう辺が、それぞれ等しい。(証明) 3 2組の向かいあう角が、それぞれ等しい。(証明)②平行四辺形の2組の対角は それぞれ等しい ③平行四辺形の対角線は それぞれの中点で交わる abcdの対角線の交点oを通る直線が 辺ad tbcと交わる点をそれぞれ m t nとする このとき mo=noであることを証明 しなさい z証明 { aomと conにおいて 平行線の錯角は等しいからad//bcより ∠mao=∠nco・・平行四辺形とひし形の違いってなに??←今回の記事 平行四辺形の角度、辺の長さを求める問題を解説! 平行四辺形の中から面積の等しい三角形を見つける問題を徹底解説! 等積変形三角形の面積問題と作図のやり方は?証明問題も紹介!




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
7・平行四辺形の面積 5年 平行四辺形って? まず、平行四辺形と言うのはどういう四角形なのか、おさらい。 2組の対辺(向かい合った辺)が平行な四角形を平行四辺形と言います。参考:「その13図形の性質と集合・四角形」。 そして、覚えておいてほしい名前など。平行四辺形の定義は、「\(\boldsymbol{2}\) 組の向かい合う辺が平行な四角形を平行四辺形という 」になります。また、平行四辺形になるためには、定義を含めて \(\boldsymbol{5}\) つの条件 があります。 平行四辺形の条件 ある平面図形が平行四辺形であるための条件には、次の \(5\) つがあります。 このうちどれか \(1\) つでも条件を満たせば、その図形は平行四辺形と言えます。 条件①2 組の向かい合う辺が平行である これは平行四辺形の定義と同じ



中2数学 平行四辺形の証明のポイントと練習問題 Examee




平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori
準備 速度の平行四辺形 与えられた時間(例えば1秒)で粒子がaからbへの線(図2)に沿って一定の速度で移動し、同時に線abがabの位置からdcの位置に一様に移動し、終始元の方向と平行なままであるとする。 両方の運動を考慮すると、粒子は線acをたどる。与えられた時間内の変位は速度の The latest tweets from @paparallelogram平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の面積sは 〔底辺〕×〔高さ〕 で求めることができる。これは平行四辺形を面積を変えずに長方形に変形させることで説明できる 。




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット



1
例文 6つの同一の面(菱形か 平行四辺形 )でなす平行六面体 例文帳に追加 a parallelepiped bounded by six similar faces (either rhombuses or parallelograms) 発音を聞く 日本語WordNet >>例文の一覧を見る 「平行四辺形」の英訳に関連した単語・英語表現 1 parallelogram (日英平行四辺形の頂点の座標 平行四辺形の性質を利用して、頂点の座標を求める方法を学びましょう。 点A(-1,3)、点B(3,3)、点C(5,-1)、点D(x,y)の4つの点を頂点とする平行四辺形ADCBがあるとき、点Dの座標を求めなさい 平行四辺形平行四辺形の定義 ①定義 2組の対辺がそれぞれ平行である。 ②定理 2組の対辺がそれぞれ等しい。 ③定理 2組の対角がそれぞれ等しい。
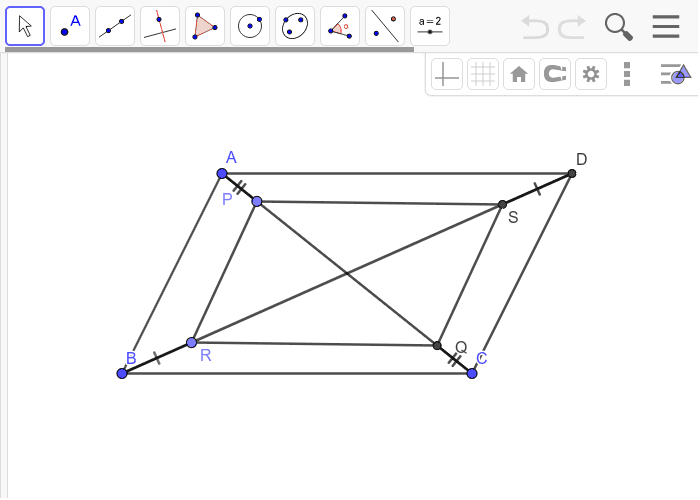



平行四辺形になるための条件 例 Geogebra




四角形 Ict教材eboard イーボード
右の平行四辺形で,辺アイ,アエはそれぞれ何cmでしょう。 また,角ア,ウ,エの角度はそれぞれ何度でしょう。 角ウ (2)ひし形 向かい合った1組の辺が平行な四角形を といいます。 向かい合った2組の辺が平行な四角形を といいます。 台形 平行四辺形の向かい合った辺の 長さは等しくなっ平行四辺形 (へいこうしへんけい、英 parallelogram)とは、2組の対辺がそれぞれ 平行 である 四角形 のことである。 表 話 編 歴 多角形 辺の数 1–10 一角形 二角形四角形 平面図形 幾何 数学 平行四辺形 難問に挑戦しよう! ブック Bunryu Kamimura How to draw the TOKYO Olympic emblem ワークシート Geo_Math_Room 折り返してできる図形2 ワークシート Geo_Math_Room 中2 平行四辺形(特別な平行四辺形) ワークシート kageyama 力の平行四辺形とてこの原理 ブック Bunryu
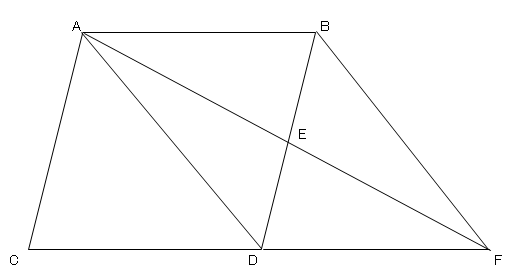



平行四辺形の証明 2 ネット塾




中2 数学 平行四辺形になるための条件 なんでこうなるのかが わかりません Clear
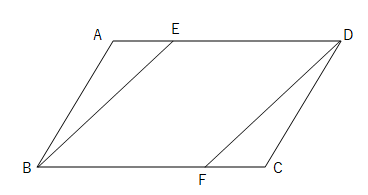
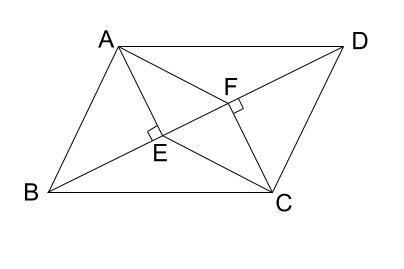
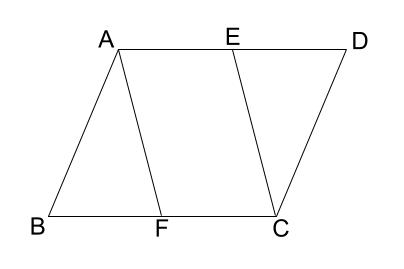
∠bae=∠dcf(平行四辺形の対角)・・・ ⑥ ④⑤⑥ より1組の辺とその両端の角がそれぞれ等しいので abe≡ cdf (2) 四角形ebfdにおいて ae=cf((1)より合同な図形の対応する辺)・・・① ad=cb(平行四辺形の対辺)・・・② ed=adae・・・③ fb=bccf・・・④ ①②③④よりed=fb・・・ ⑤ ad//bc(平行四辺形の対辺) 平行四辺形になる条件は、言葉だけでなく図形とセットで覚えるのがポイントです。 では、以上のことを踏まえて次の問題を解いてみましょう。 問題:次の(1)~(4)のうち、平行四辺形であるといえるものを選びなさい。 (1) ad=5 ㎝、bc=5 ㎝、ab//cd の四角形 abcd② 垂直,平行や台形,平行四辺形,ひし形の弁別や作図ができるようになる。 ③ 垂直,平行や台形,平行四辺形,ひし形の概念とそのかき方を理解する。 この学習内容は第4学年の内容C(1)平行四辺形,ひし形,台形のア,イにかかわるものである。
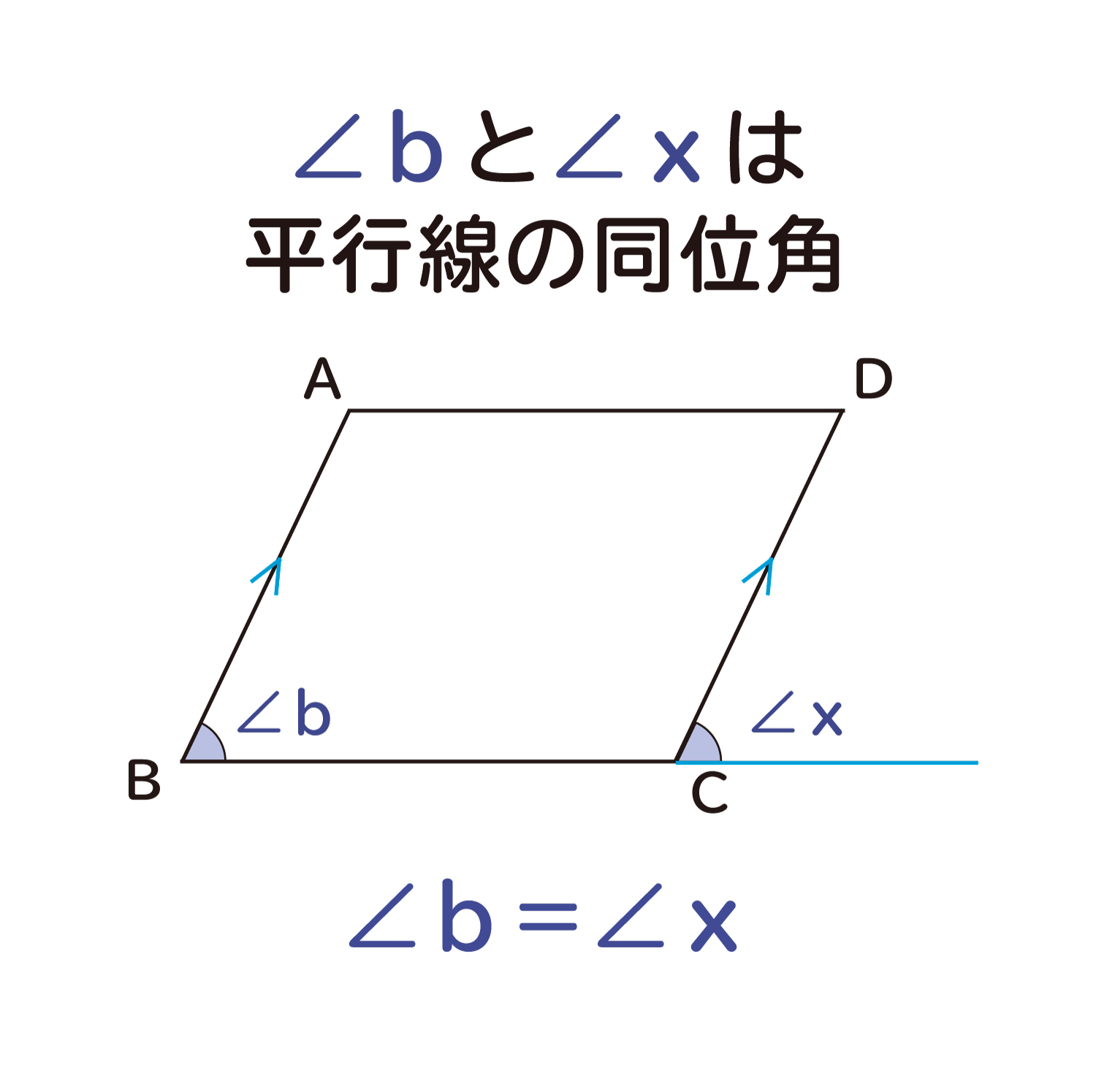



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
行列式 線型代数 数学教育 二つのベクトル v 1, v 1 が張る平行四辺形の面積を考える: v 1, v 1 を数ベクトルに表す: 平行四辺形の面積は,つぎの計算で求められる: (a 11 + a 21 ) × (a 12 + a 22 ) ー( a 11 × a 12 + a 21 × a 22 + 2 × (a 12 × a 21) ) = a 11 × a平行四辺形の対角線CE)の過小視の組 F E'・ D' ・ み合わせにより生じた。 。 さて,本論の実験は, Metzgerの説を Fig 1ザンダーの平行四辺形(ザンダー錯視) さらに精神物理学的に検討するために計, 画された。平行四辺形は,長短二本の対角線を持ち,長い方の対角線は長対角線,短い方平行四辺形の角度、辺の長さ まとめ お疲れ様でした! 平行四辺形の角度、辺の長さ問題では そこまで『難しい』と困ってしまうようなものはありませんね。 平行四辺形の基本性質を覚えておくだけで簡単に解けるものばかりです。 平行四辺形の基本性質
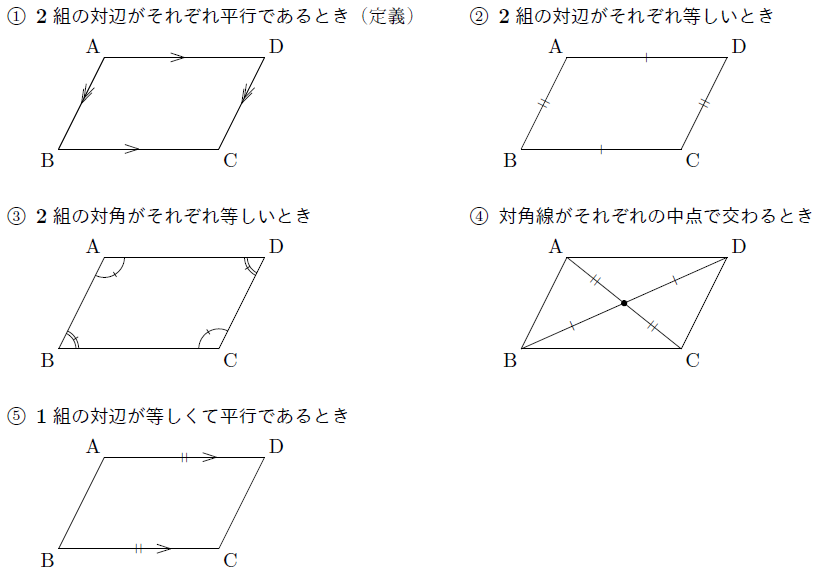



平行四辺形になるための条件 まなびの学園




平行四辺形の辺や角を求める Youtube
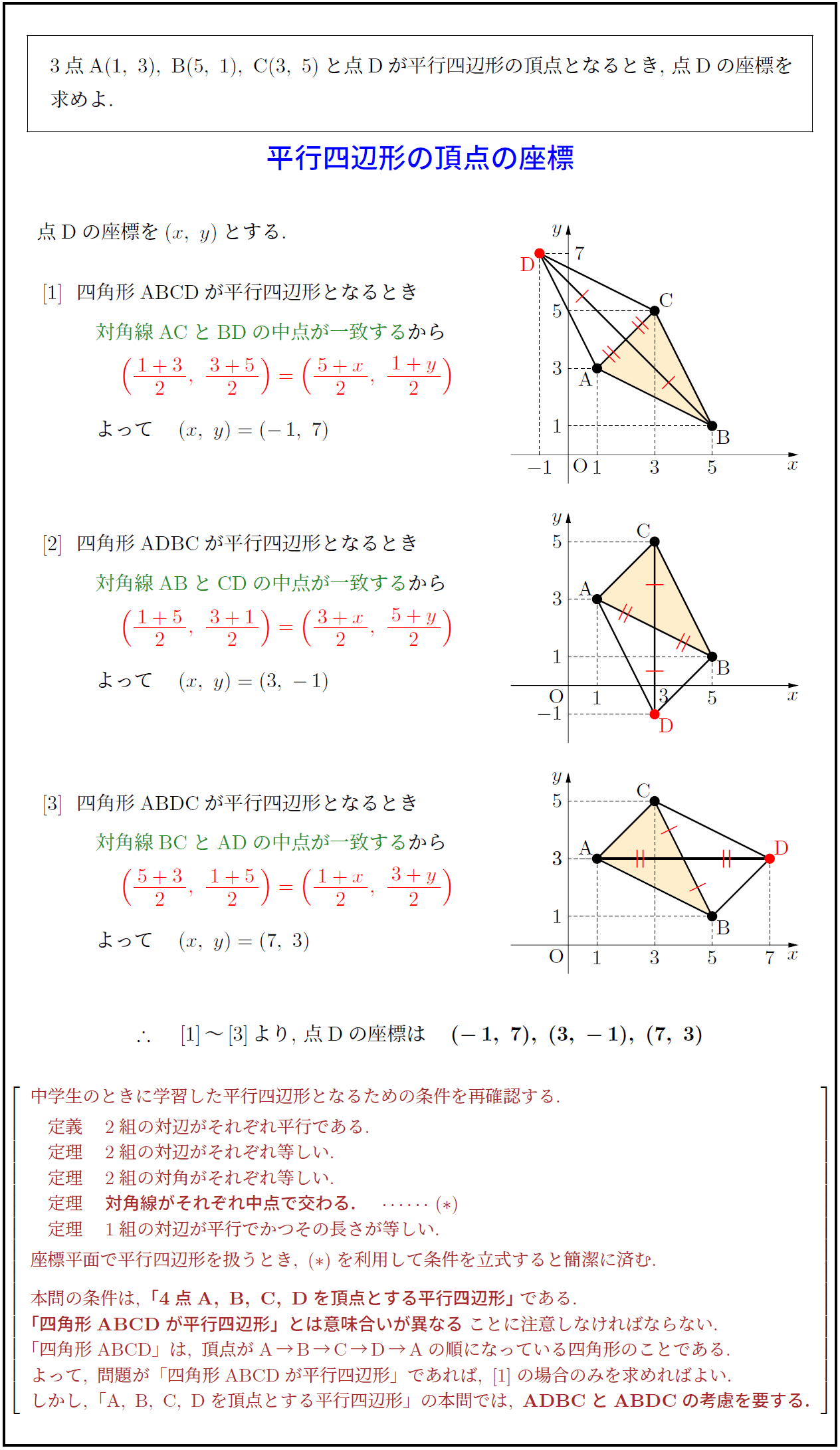



高校数学 平行四辺形の頂点の座標 受験の月
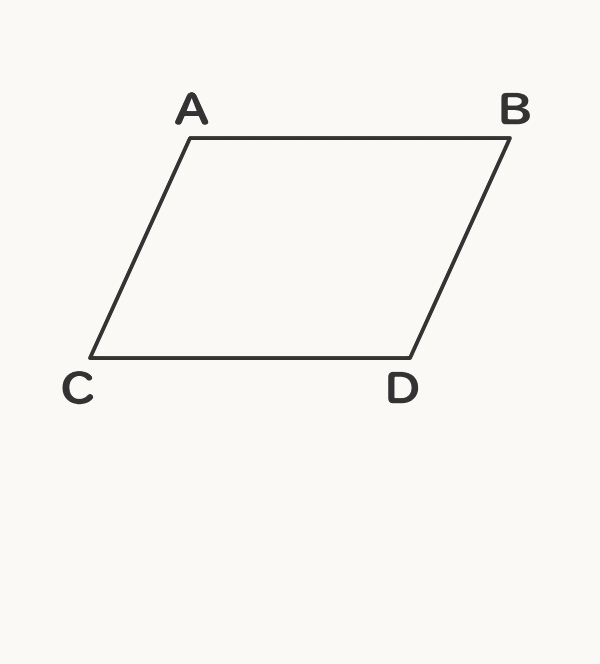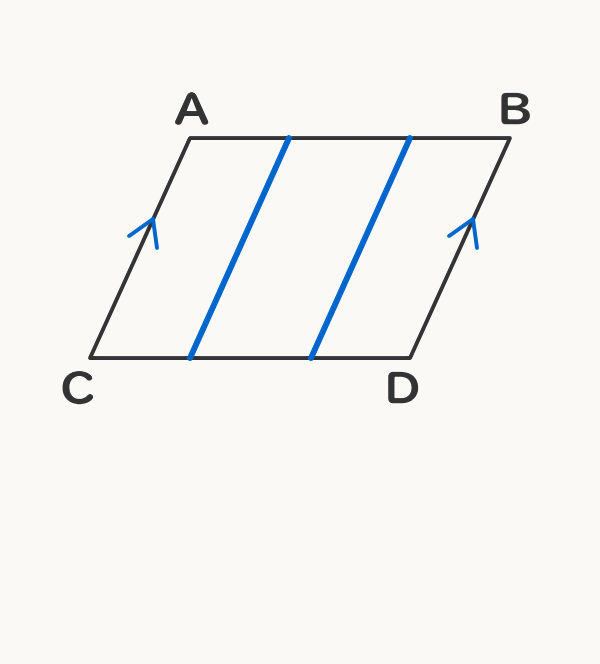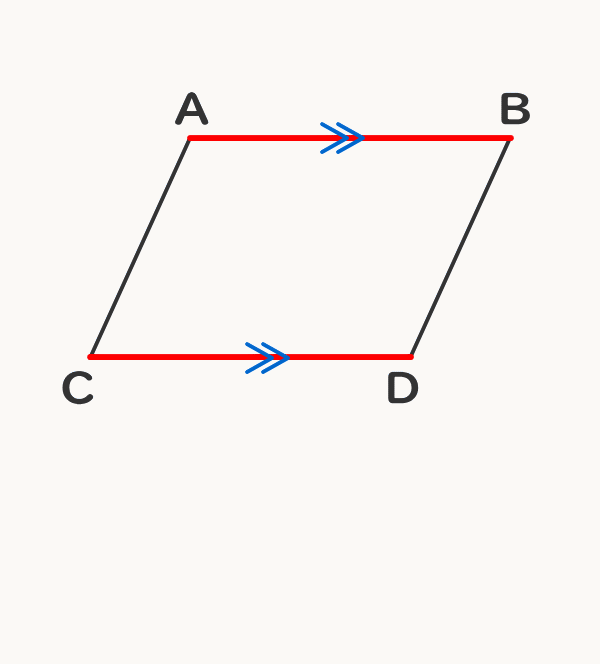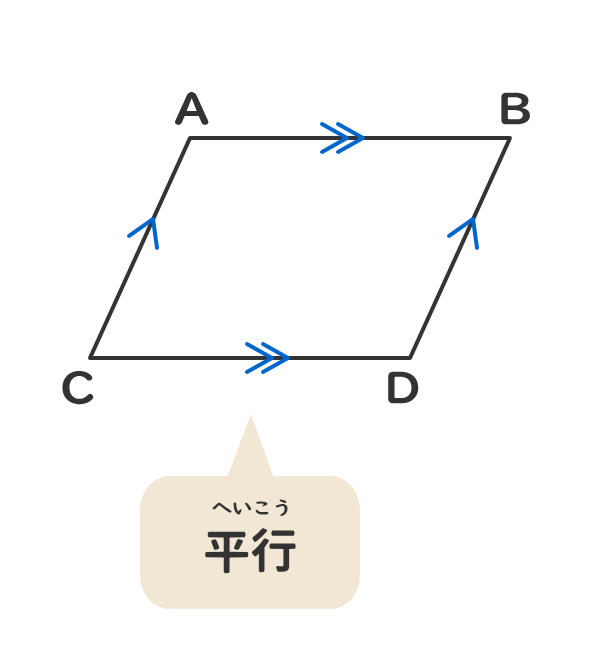



平行四辺形の仲間を知ろう 電験3種web




平行四辺形の面積の求め方 公式と計算例




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




平行四辺形で知っておくべきこと 苦手な数学を簡単に



平行四辺形の性質を使った証明 平行四辺形になることの証明 チーム エン




中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu



今月の問題 平行四辺形



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生



平行四辺形の家 A Sa Araki Sasaki Architects



平行四辺形の面積の公式 算数の公式
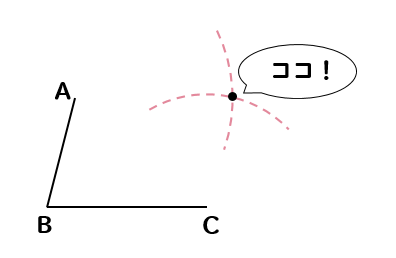



平行四辺形の書き方 コンパスを使って作図する方法は 数スタ




2次の正方行列式と平行四辺形の面積 機械学習に詳しくなりたいブログ




台形と平行四辺形の定義 ちがい 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の 苦手を克服



平行四辺形の性質1




平行四辺形の仲間を知ろう 電験3種web
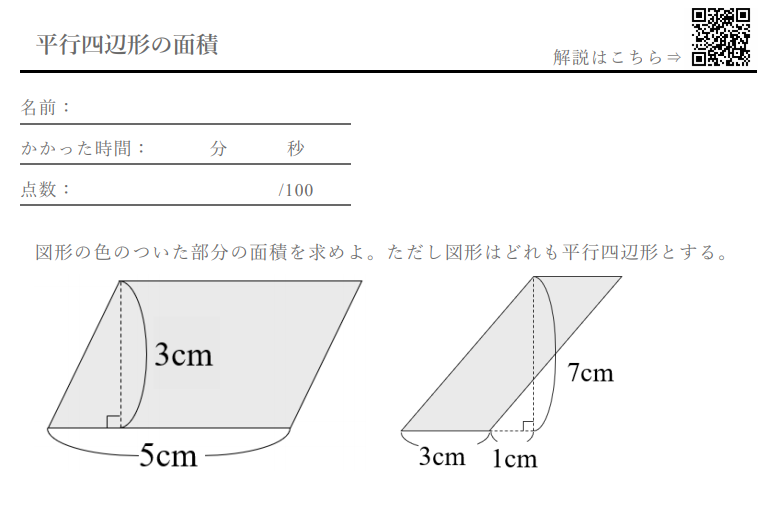



平行四辺形 の面積 計算ドリル 問題集 数学fun
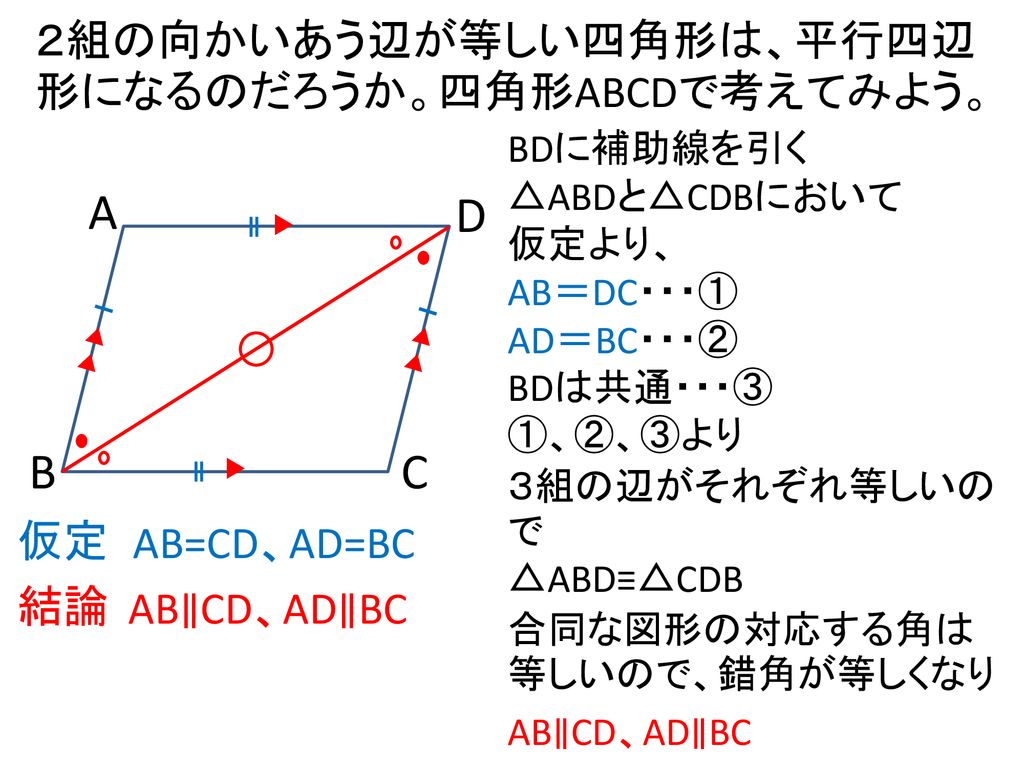



ねらい 平行四辺形の性質の逆を証明し 平行四辺形になるための条件を導くことができる Ppt Download




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室
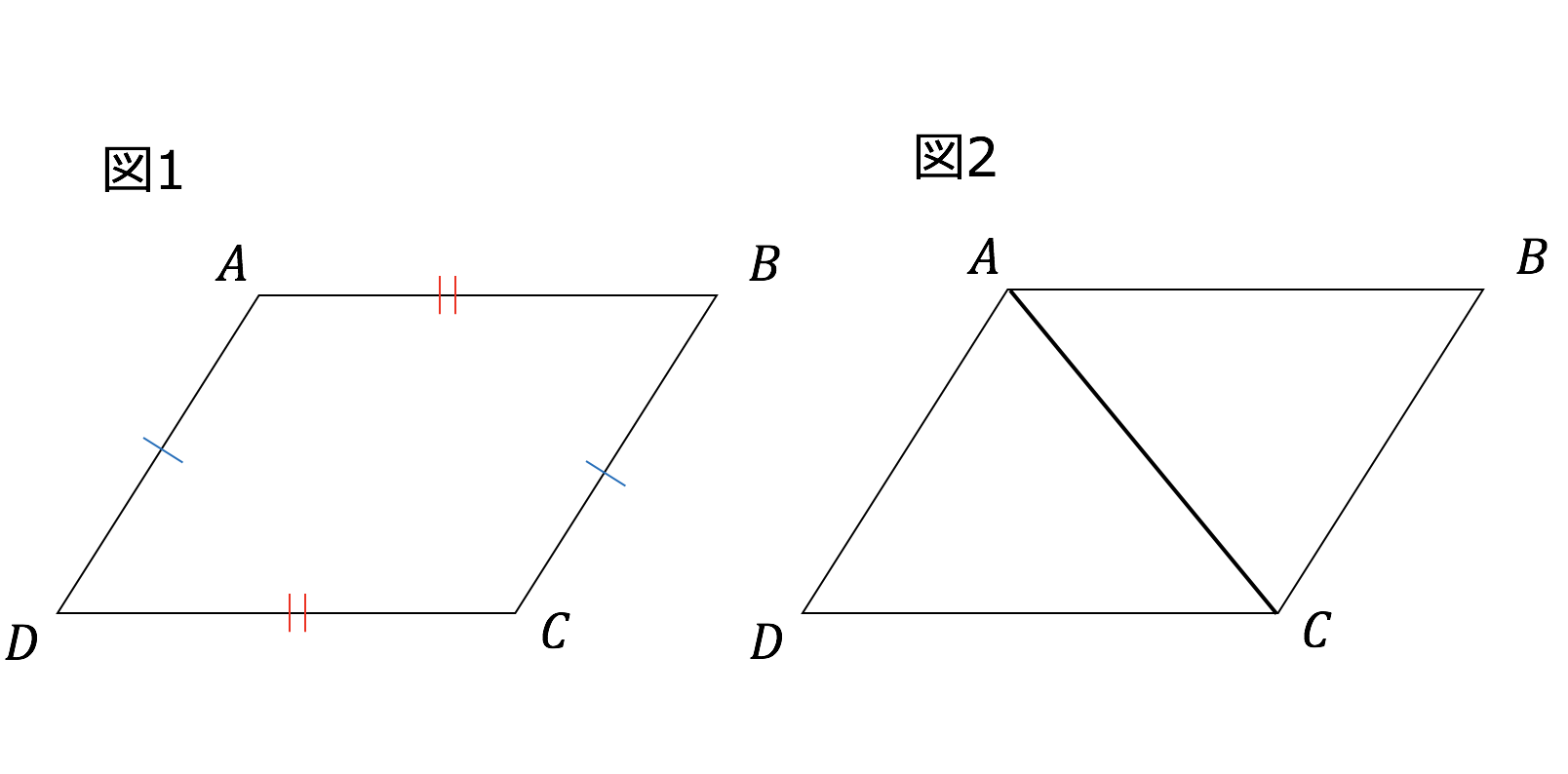



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ




平行四辺形の対角線の長さの求め方




平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su
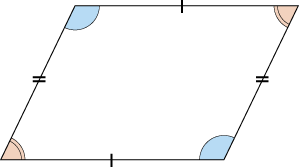



平行四辺形の性質 5年生 算数の広場



特別な平行四辺形2
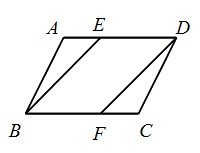



Math 平行四辺形 平行四辺形になることの証明 働きアリ



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル




平行四辺形の辺や角を求める Youtube




平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ
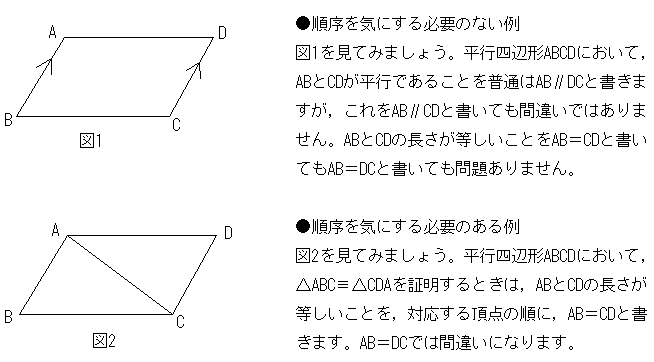



三角形と四角形 平行四辺形の辺や角の表記の順序 中学数学 定期テスト対策サイト




3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ




平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題




平行四辺形 は英語で何と言う 四角形の名前




平行四辺形の定義と性質 証明問題の解き方 数学fun
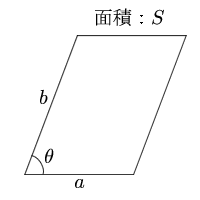



平行四辺形 2辺と間の角度 面積の計算 計算サイト



平行四辺形になる条件




File 平行四辺形の面積1 Png Wikimedia Commons




数学 中2 74 平行四辺形になる条件 Youtube
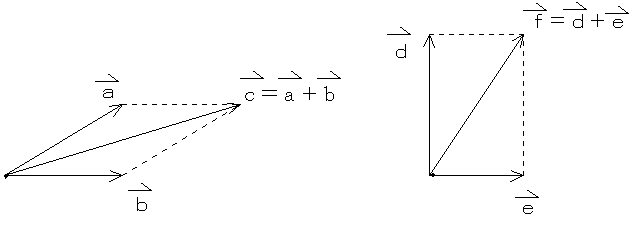



力の平行四辺形




平行四辺形と証明 Youtube



中学2年数学練習問題 図形と合同 平行四辺形の性質と証明問題




中2数学 平行四辺形の証明の定期テスト予想問題 Pikuu




スクラッチの簡単なプログラム例 小学校算数 しきつめ 平行四辺形編
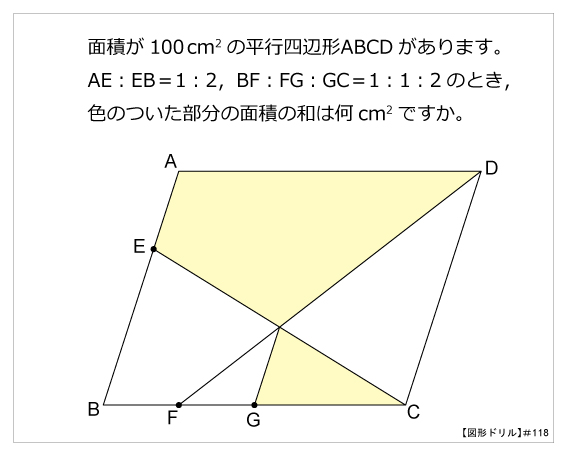



図形ドリル 第118問 平行四辺形の面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦




標準 平行線と平行四辺形の個数 なかけんの数学ノート



数学 中2 73 平行四辺形の性質 Youtube
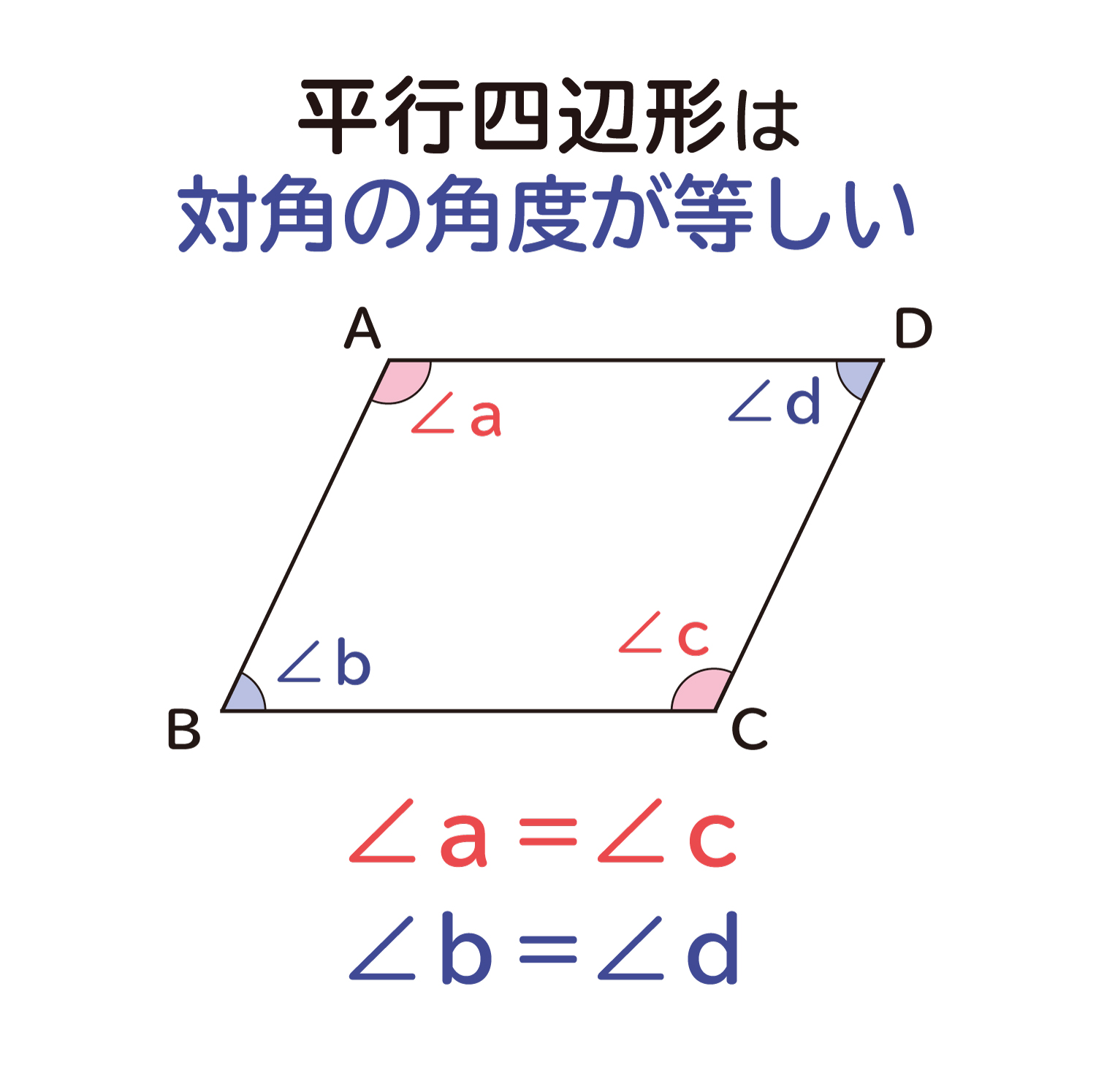



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル




平行四辺形の面積の求め方 公式と計算例




File 平行四辺形の面積2 Png Wikimedia Commons
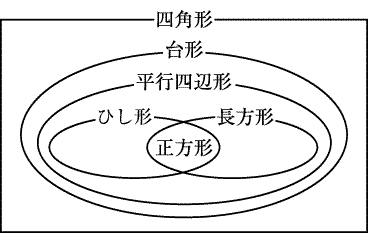



図形の包摂関係 算数用語集




File 平行四辺形の性質 2 Png Wikimedia Commons
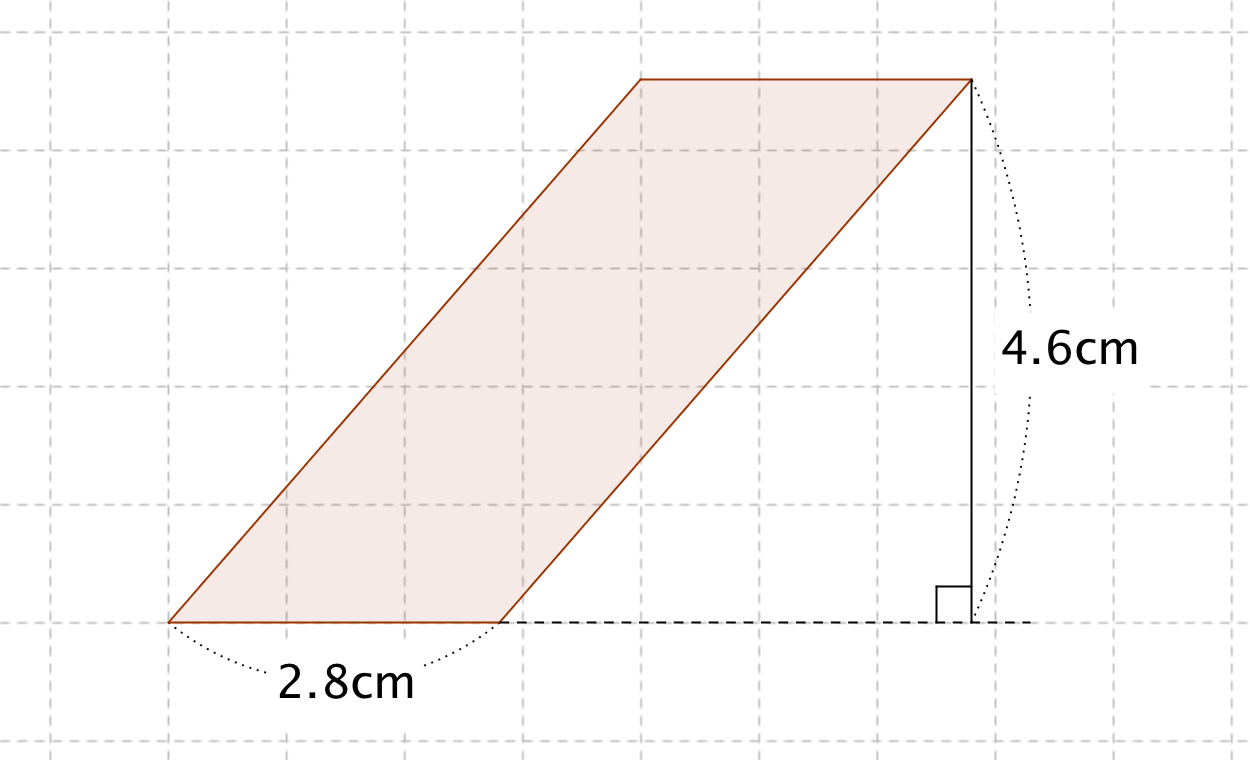



平行四辺形の面積の公式 算数の公式
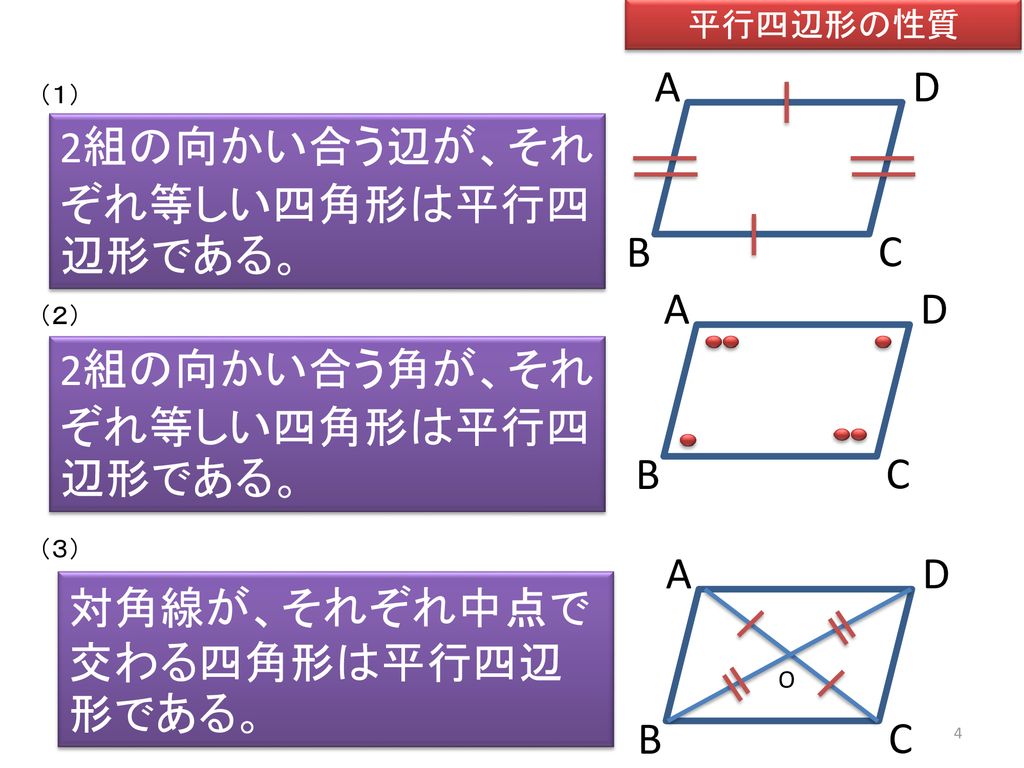



平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download




平行四辺形 中学数学で遊ぶ 身勝手な主張



3




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




平行四辺形 へいこうしへんけい とは ピクシブ百科事典



平行四辺形になる条件
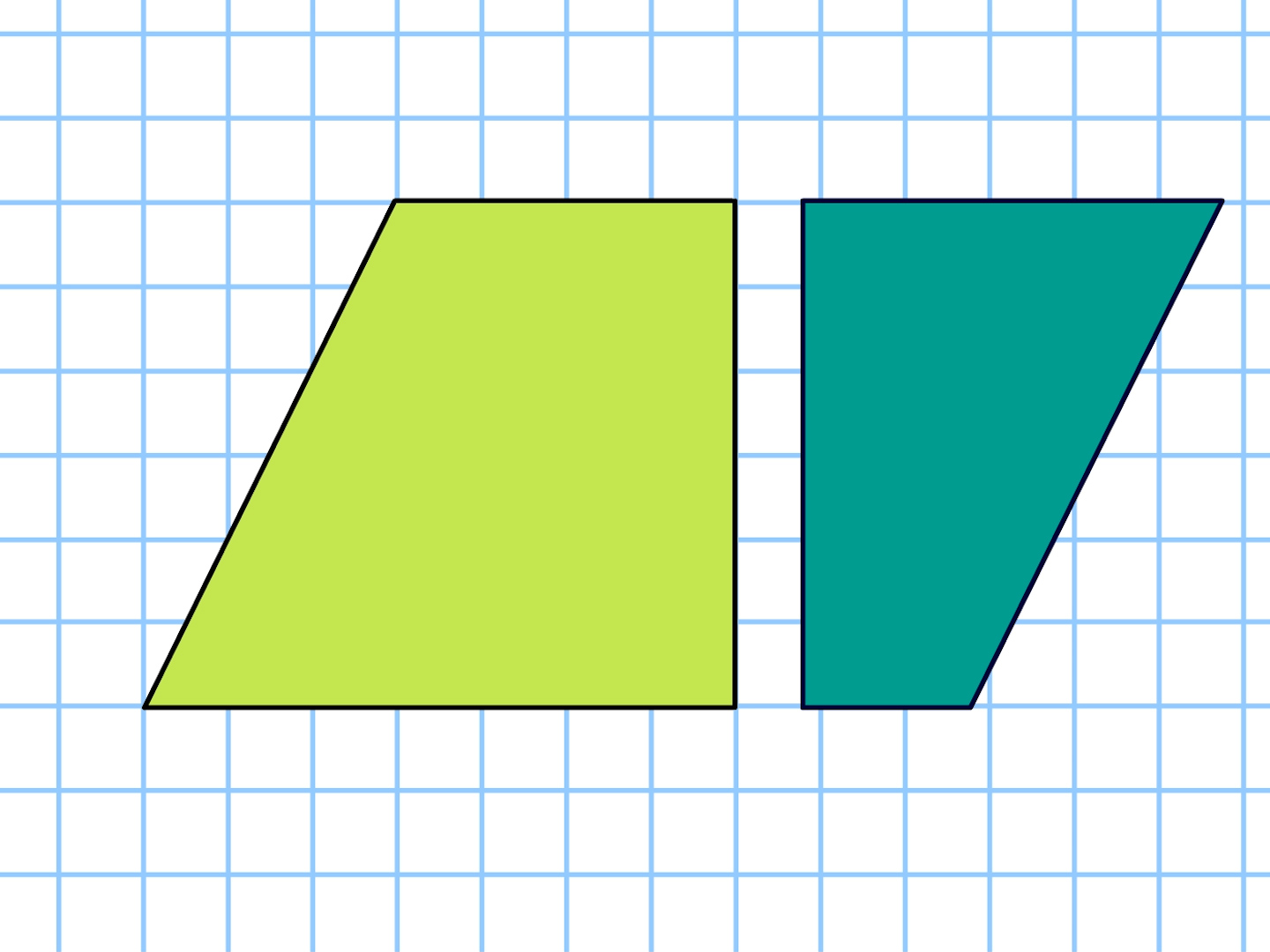



5年 平行四辺形の面積 算数イメージ動画集 大日本図書




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




標準 平行四辺形と座標 なかけんの数学ノート




平行四辺形の面積の求め方 公式と計算例




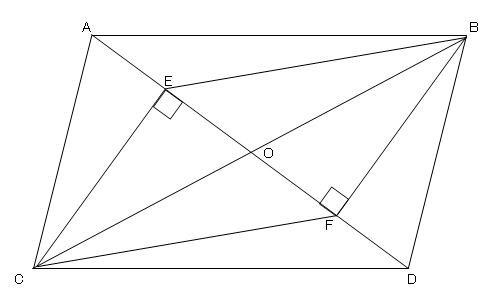
平行四辺形abcdの頂点a Cから対角線bdに垂線を引き 対角線との交点をそれぞれ Clear
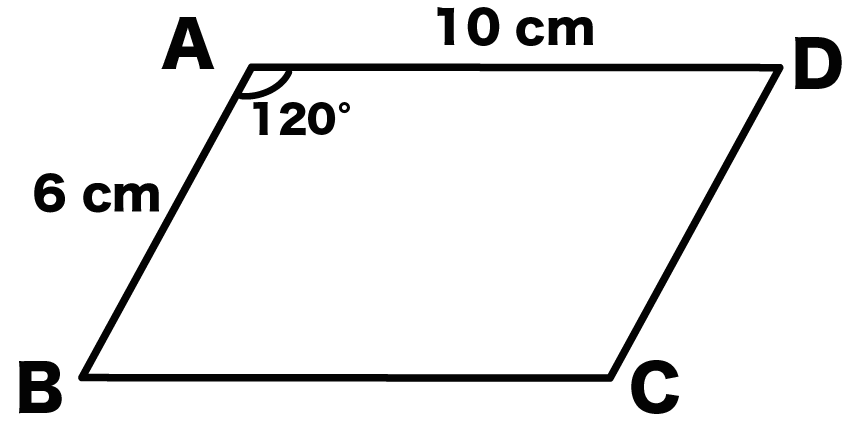



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




平行四辺形 Wikipedia
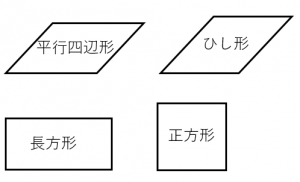



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学
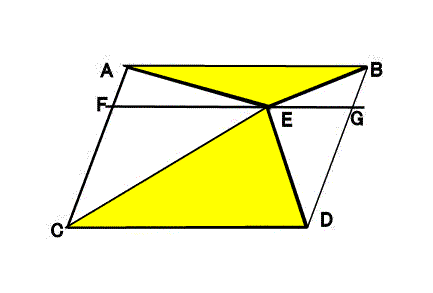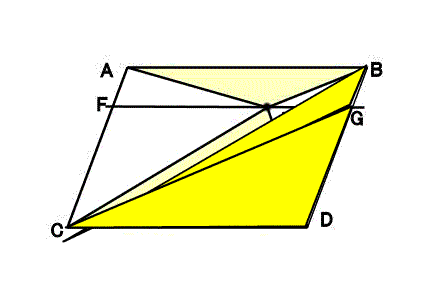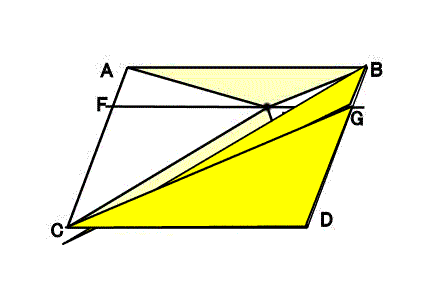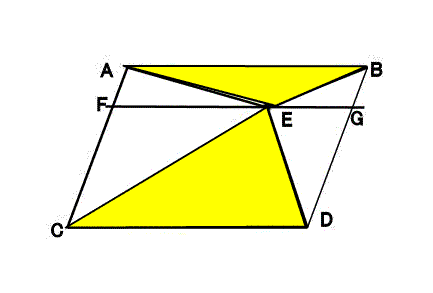



平行四辺形と三角形 1




数学も英語も強くなる 意外な数学英語 Unexpected Math English Rhomboid



平行四辺形になることの証明 On Vimeo




台形と平行四辺形を平行な辺の組の数で分類することは 原理的に不可能である 小学校4年生の算数 身勝手な主張




中2数学 平行四辺形であるための条件 例題編 映像授業のtry It トライイット



3




平行四辺形になるための条件 Youtube




Math 平行四辺形 平行四辺形になることの証明 働きアリ




高校数学b ベクトルの成分表示と平行四辺形 受験の月




平行四辺形の証明問題 無料で使える中学学習プリント



平行四辺形の証明 4 ネット塾
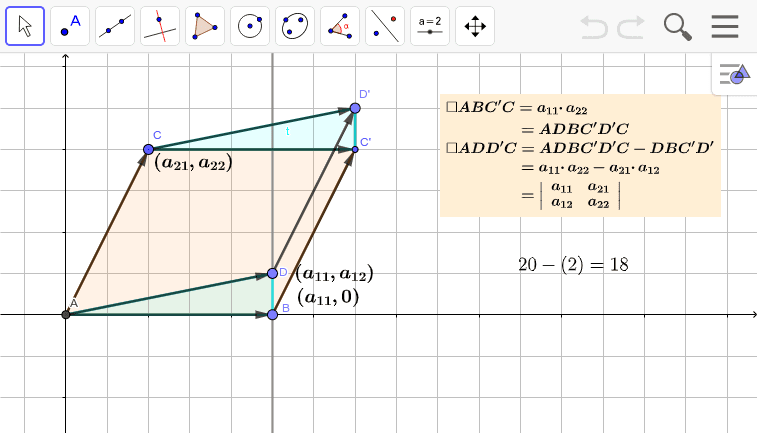



平行四辺形の面積と行列式 Geogebra



平行四辺形の家 A Sa Araki Sasaki Architects




3分でわかる 平行四辺形の定義とは Qikeru 学びを楽しくわかりやすく




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題



平行四辺形について知ろう 苦手な数学を簡単に




File 平行四辺形の説明 Png Wikimedia Commons
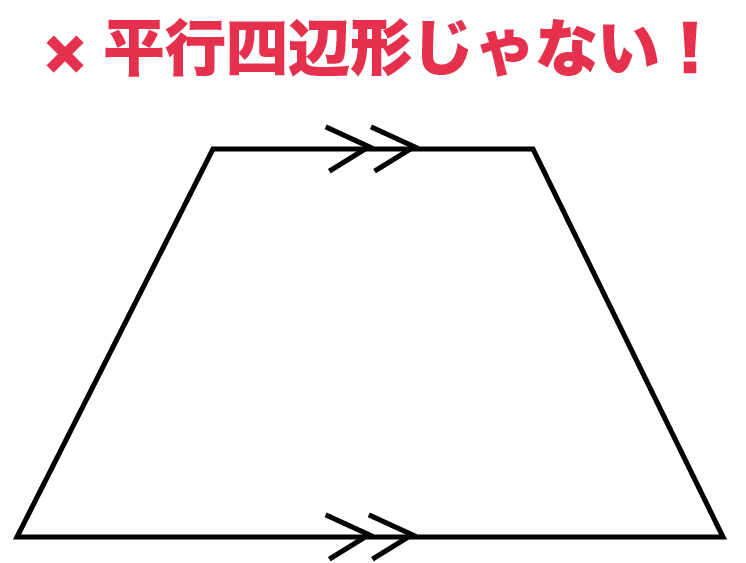



3分でわかる 平行四辺形の定義とは Qikeru 学びを楽しくわかりやすく




平行四辺形の面積の求め方 公式と計算例




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1



0 件のコメント:
コメントを投稿