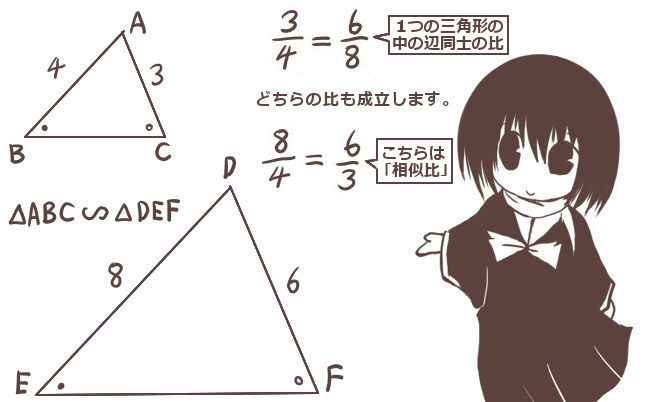
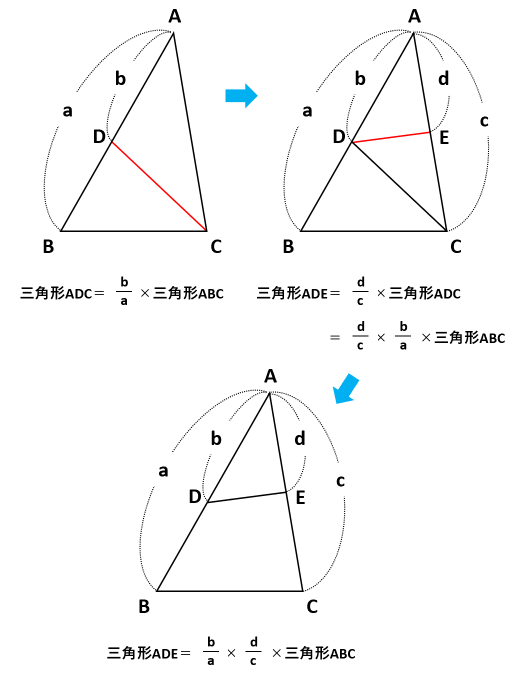
三角形の内角・外角の二等分線と辺の比の関係とその証明 三角形の角の二等分線と辺の比Aの二等分線と辺BCの交点P}}は,\ 辺BCを\ \syoumei\ \ 直線APに平行な直線を点Cを通るように引き,\ 直線ABの交点をDとする (右図) (同位角), (錯角)}$ \\ 2zh \phantom { (1)}\ \ 仮定※この定理はd, eが辺ba, caの延長上にあっても成り立つ。 定理の証明 ① abcと adeにおいて de//bcより、平行線の同位角は等しいので ∠abc=∠ade, ∠acb=∠aed よって2組の角がそれぞれ等しいので abc∽ ade 相似な三角形の対応する辺の比は等しいので adab=aeac=debc ② 直角三角形abcにおいては、 bd:dc=ab²:ac² でした。 したがって、 bd:dc=169:81 です。 2乗すればいいだけですね。簡単です。 三平方の定理など他にもいくつかの方法で解くことができますが、これを知っていれば数秒で終わります。

交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー
三角形 辺の比 平行
三角形 辺の比 平行-$15^\circ$ の三角比の値は覚えなくてもよいが、$15^\circ$ を含む直角三角形から導けるようにしておこう。 これらの角以外にも、$18^\circ$、$36^\circ$、$72^\circ$、$144^\circ$ などの角も、特殊な三角形を考えることによって三角比を 求めることができる。三角形の相似条件は、次の3つがあります。 3組の辺の比がすべて等しい 3組の辺の比がそれぞれ等しい三角形 「3組の辺の比が等しい」とは、上の2つの三角形で \ aa'=bb'=cc' \ が成り立つことをいいます。 この条件を、3辺比相当( SSS SideSideSide )とも




黄金三角形による18 シリーズの三角比 おいしい数学
平行線と線分の比 平行線と線分の比 1 pq//bc ⇔ apab = aqac 2 pq//bc ⇔ appb = aqqc 3 pq//bc ⇒ apab = pqbc a p q p q a b c b c ※3だけ逆は成り立たない。 角の二等分線と比 角の二等分線と比 1 abcの∠aの二等分線と辺bcとの 交点pは辺bcをabbcに内分する。 三角比の導入 三角形のうちの2辺の比というのは, 相似な三角形の対応する2辺の比においても変わらずに一定であることはご存知のことであろう 例えば, 直角三角形 \( ABC \) と \( ABC \) に相似な直角形 \( A^{\prime}B^{\prime}C^{\prime} \) について考えよう 三角形における辺の関係と考えておけば良いです。 三角比 3つの三角比を覚えておきましょう。 「 三角比 」という用語を使うのは三角形の\(\,3\,\)辺に関連しているからなので、 三角形を書きながら見ていくとわかりやすいです。 正弦、余弦、正接
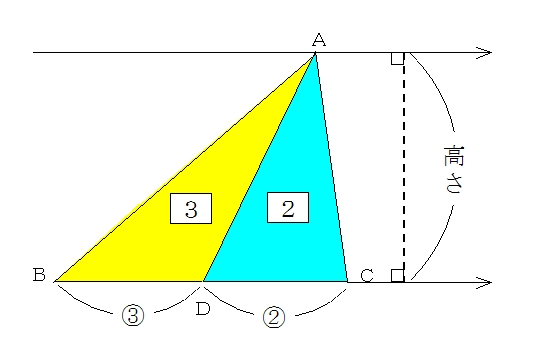
三角形ABE と 三角形ACE はAEが共通で、この辺が底辺になります。 つまり、この2つの三角形の面積比は、"高さ"に等しくなります。 BDとDCの比がどうして、"高さ"の比に等しくなるのか考えてみま三角比を求められるようにしておきましょう。 30° 45° √3 1 1つの角が 30° である直角三角形の辺の比は 1∶2∶√3 となっているので,sin30°= また,1つの角が 60° である直角三角形の辺の比も同様なの図形と計量三角形の辺の長さを求めるときの三角比の値 xの値を求めよ。という問題で, これを解こうとすると,sin45°,sin60°という三角比が出てきました。 定義では,「直角三角形」だけで考えるとありました。
先ほど確認したとおり、三角形の面積は「(底辺)×(高さ)× 1 2 1 2 」です。 底辺の比は、相似比なので、1:2。 高さの比も相似比と同様に1:2ですね。 どちらの三角形の面積も 1 2 1 2 をかけるので、△ABC:△A'B'C'=1×1:2×2=1=4となります。三角形と比 三角形と比 三角形の一辺に平行な直線をひいた時にできる線分の比 について考えていこう。 辺AB を 4等分 するように 点D、E、F をおいてある。 直線は 3点 から 辺BC に平行になるようひいてあるよ。 AD:DE:EF:FB=1:1:1:1 となっている直角三角形である。 (2) 9cm, 8cm, 4cm 9が最も長いのでc 2 = 81 a 2 b 2 = 64 16 =80 よってa 2 b 2 ≠ c 2 となるので 直角三角形ではない。 確認 次の長さを3辺とする三角形のうち、直角三角形をすべて選べ。 答表示




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく
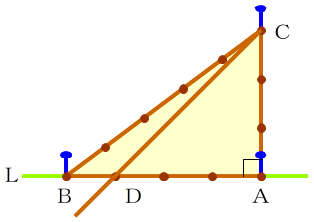



3 4 5の三角形で 本当に直角ができる Note Board
三角形の面積比(等高, 等底, 等角) 高さが同じ三角形の面積比\ →\ 底辺の比底辺が同じ三角形の面積比\ →\ 高さの比 角が同じ三角形の面積比\ →\ 角を挟む辺の積の比 等高と等底については中学で学習済みであるが,\ について少し補足しておく (相似 このときの三角形の辺の2つの辺の比のことを 三角比 と言う。 ある1つの基準となる角度に対して、どの辺とどの辺を使った三角比なのかによって、サイン、コサイン、タンジェントと呼び方が変わってくる。 二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう! 「サイト内お気に入り」に登録する 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な



三角形の相似 理数系無料オンライン学習 Kori




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
角度θを決めると「直角三角形の辺の長さの比」は決まるので,これらの比は角度θの関数であると言えますが, 今までに習った1次関数 3θ ,2次関数 θ 2 3θ4 などでは表せないことが分かっています.そこで「直角三角形の辺の長さの比を表す新しい関数の 1 数学三角形の辺と面積の比について、2つの考え方をサクッとまとめました中学数学 図形 11 三角形の線分比と面積比の関係①;辺の長さの比1:1:√2 60°と30°の直角三角形です。 いちばん長い辺はいちばん短い辺の2倍の長さ です。 辺の長さの比1:2:√3




中学3年数学練習問題 三角形の比 辺の長さを求める問題 図形と相似




直角三角形の角から垂線を引いたときの底辺の比の問題 の裏ワザ 大阪のプロ家庭教師が できない を できる に変える
こちら の記事で説明したように、 三角形の面積比は「(底辺の比)×(高さの比)」 で求めます。平行線と線分の比 右図2のような図形において幾つかの辺の長さが分かっているとき,未知の辺の長さを求めるために図1の黄色の矢印に沿って辺の長さを求めることができる. bd//ce のとき まず




辺の比と面積比問題 考え方1 Youtube
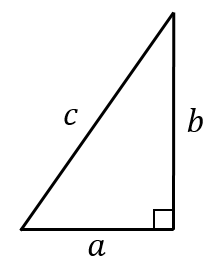



直角三角形で 3辺の比が整数になる例25個と作り方 具体例で学ぶ数学




特別な直角三角形の辺の比 無料で使える中学学習プリント




黄金三角形による18 シリーズの三角比 おいしい数学




平面図形をマスター 三角形の面積比 応用編その3
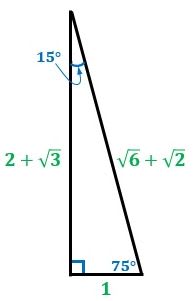



直角三角形の辺の比 東久留米 学習塾 塾長ブログ
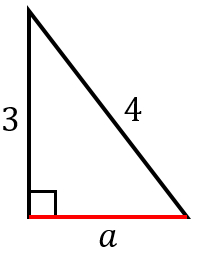



直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学
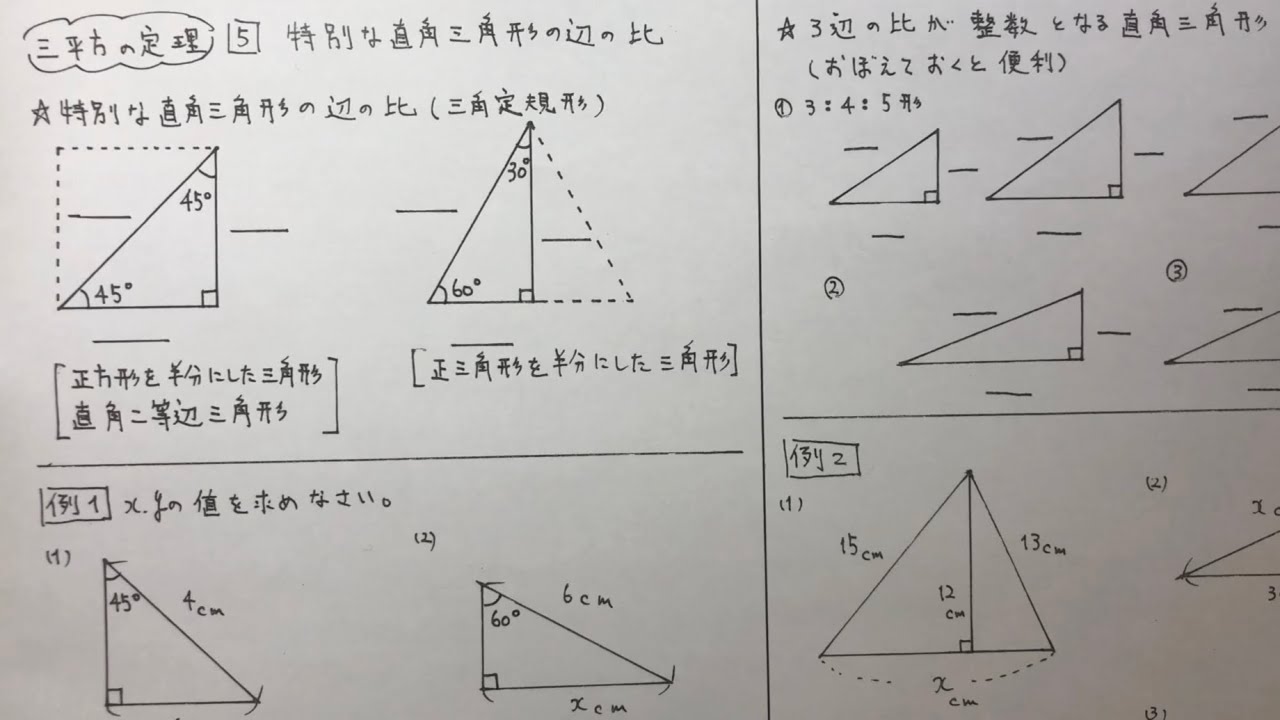



中3数学 三平方の定理5 特別な直角三角形の辺の比 Youtube




辺の比と面積比 基本編 Youtube




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中3数学 三角形の相似条件1 3辺の比 映像授業のtry It トライイット



辺の比と面積比 等角三角形 富士山型 Next Stageのブログ




三平方の定理 覚えること 三角定規 苦手な数学を簡単に
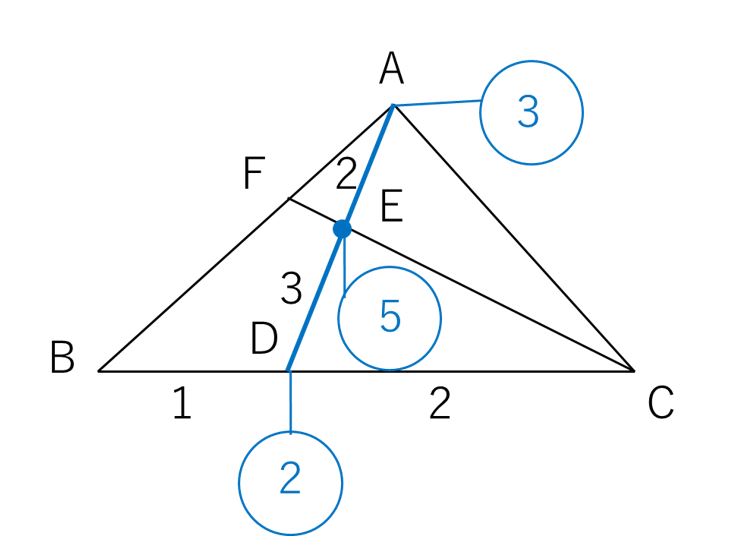



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ




平面図形をマスター 三角形の面積比 応用編その3
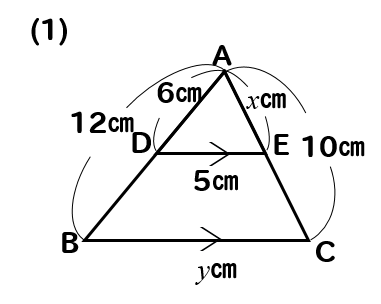



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube



Tossランド 特別な直角三角形の辺の比の復習のさせ方
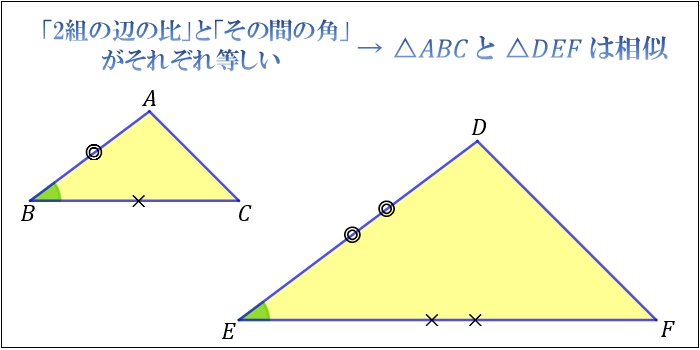



三角形の相似条件について 図解で分かる相似条件 アタリマエ




平面図形をマスター 三角形の面積比 応用編その3




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学
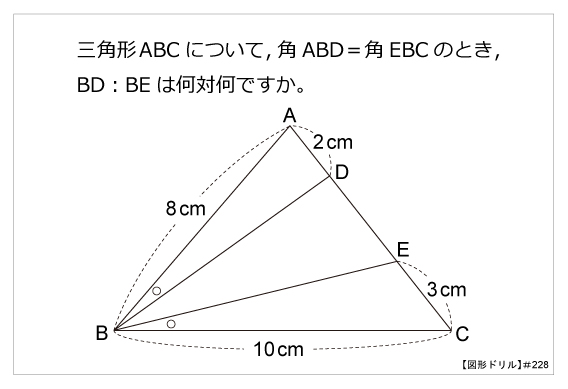



図形ドリル 第228問 等しい角度と辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー



1




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




タンジェントとは何か 中学生でも分かる三角関数の基礎




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学



三角形って辺の長さの比は3辺すべて同じ比ですよね 正 Yahoo 知恵袋




中3 三角形の相似条件 三辺比相等 日本語版 Youtube
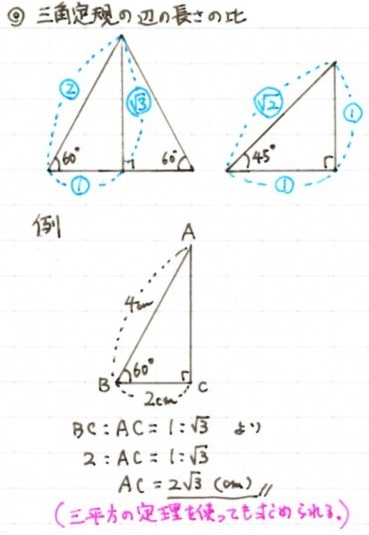



直角三角形の3辺の比 高校入試問題 数学 を毎日解いてみよう
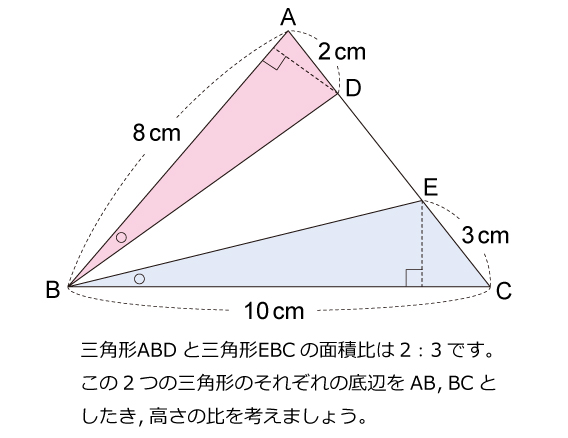



図形ドリル 第228問 等しい角度と辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦
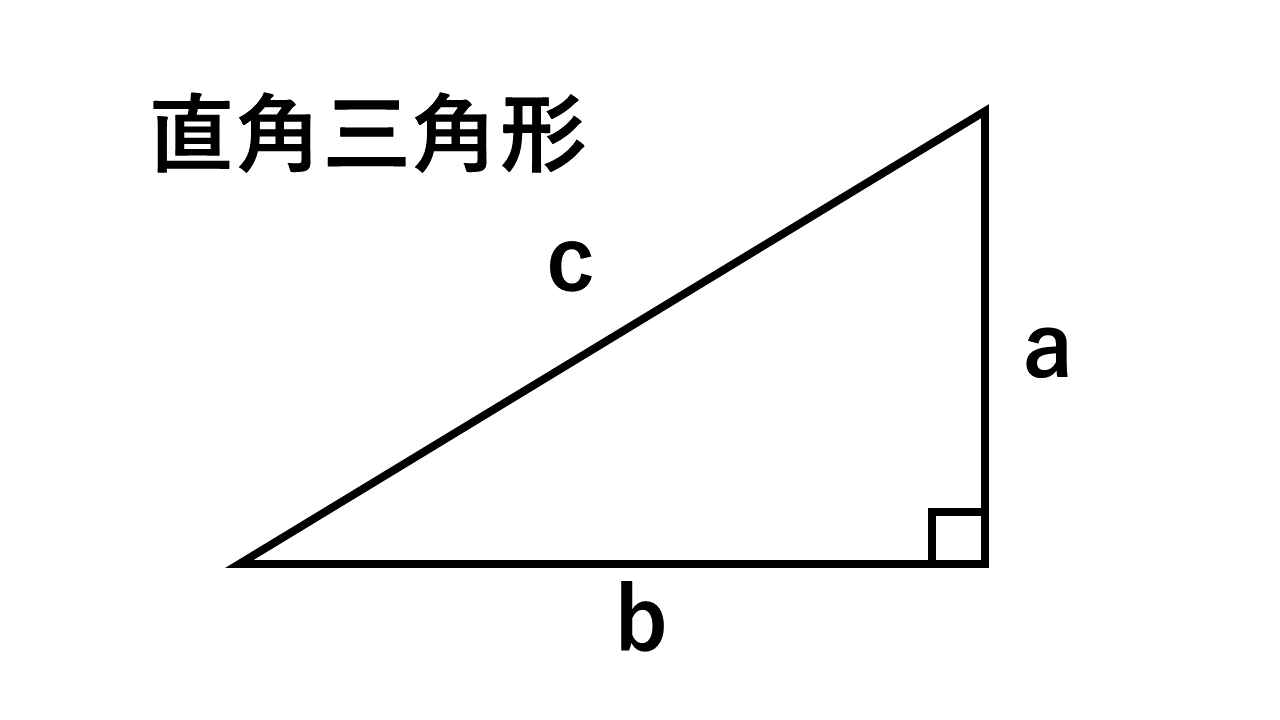



中学数学 直角三角形3 4 5以外に知ってる




三角形辺の比 Abcと線分pqが1つの平面上にある 点p Qからbc Okwave
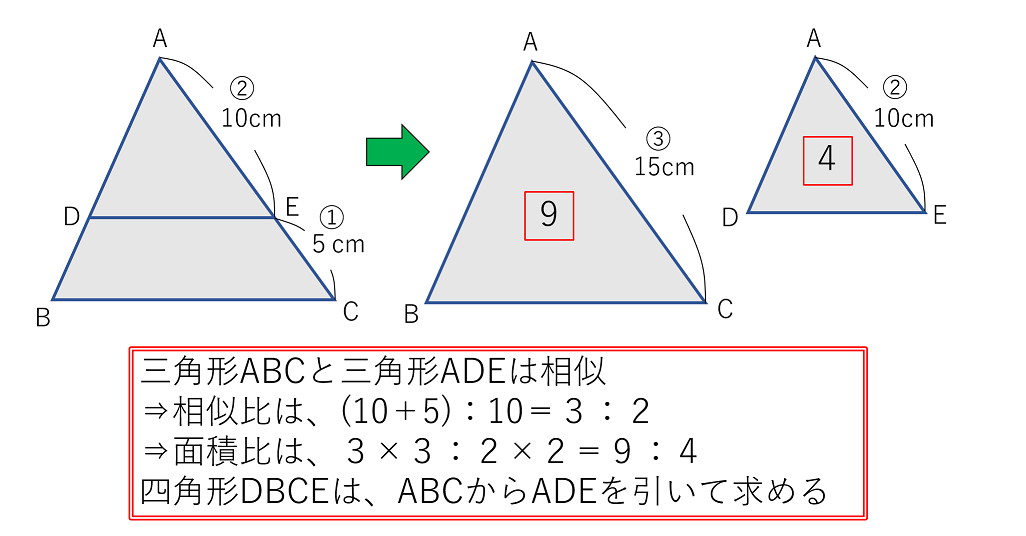



成績アップの秘訣 自学学習のススメ 数学の三角形の相似比 ピラミッド型と砂時計型 幼児教育 児童教育




三角形の面積比 数学の偏差値を上げて合格を目指す




テストによく出る直角三角形の辺の比 中学数学 By じょばんに マナペディア




平面図形をマスター 三角形の面積比 応用編その3




相似比を使って辺の長さを求める Youtube



1
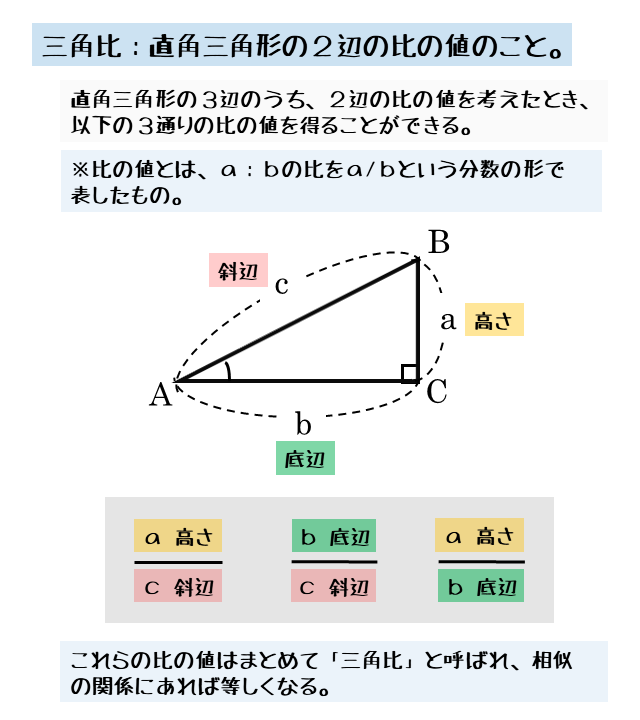



図形と計量 三角比の定義について 日々是鍛錬 ひびこれたんれん




黄金三角形による18 シリーズの三角比 おいしい数学
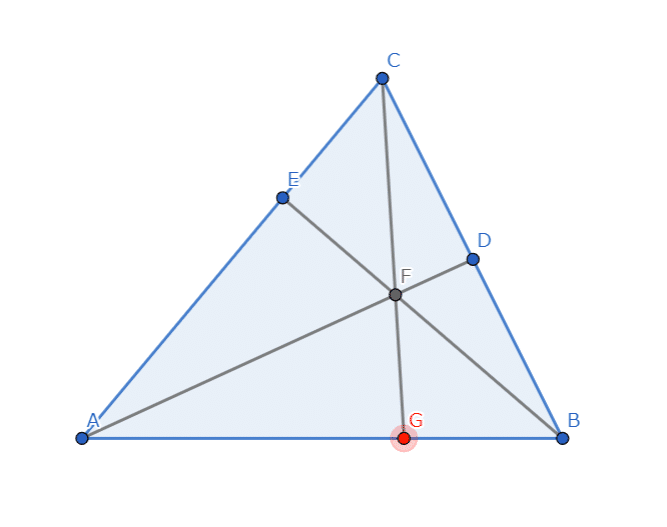



平面図形 三角形を分割した時の底辺の比とコンパスのような部分の面積の比は同じ ワンセンテンス算数 Note




Helpful Site For Study 2月 18




三角形の相似条件
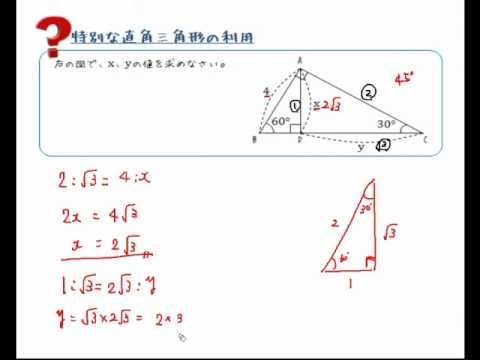



特別な直角三角形の利用 Youtube




特別な直角三角形の3辺の比 の問題が分からないんですけど やり方を教えてください Clear




黄金三角形による18 シリーズの三角比 おいしい数学




三角形で面積比と底辺の比の関係は 平面図形分野の頻出問題を考える みみずく戦略室




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



Studydoctor相似な三角形の辺の比 中3数学 Studydoctor



1




数学 三角形の辺と面積の比について 2つの考え方をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生
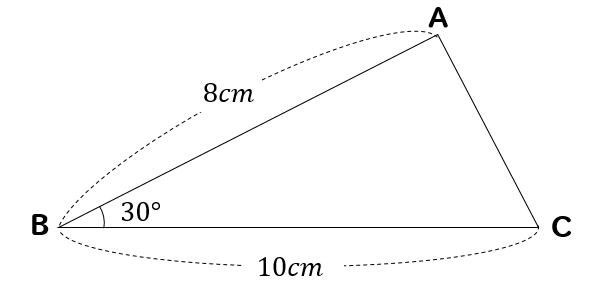



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
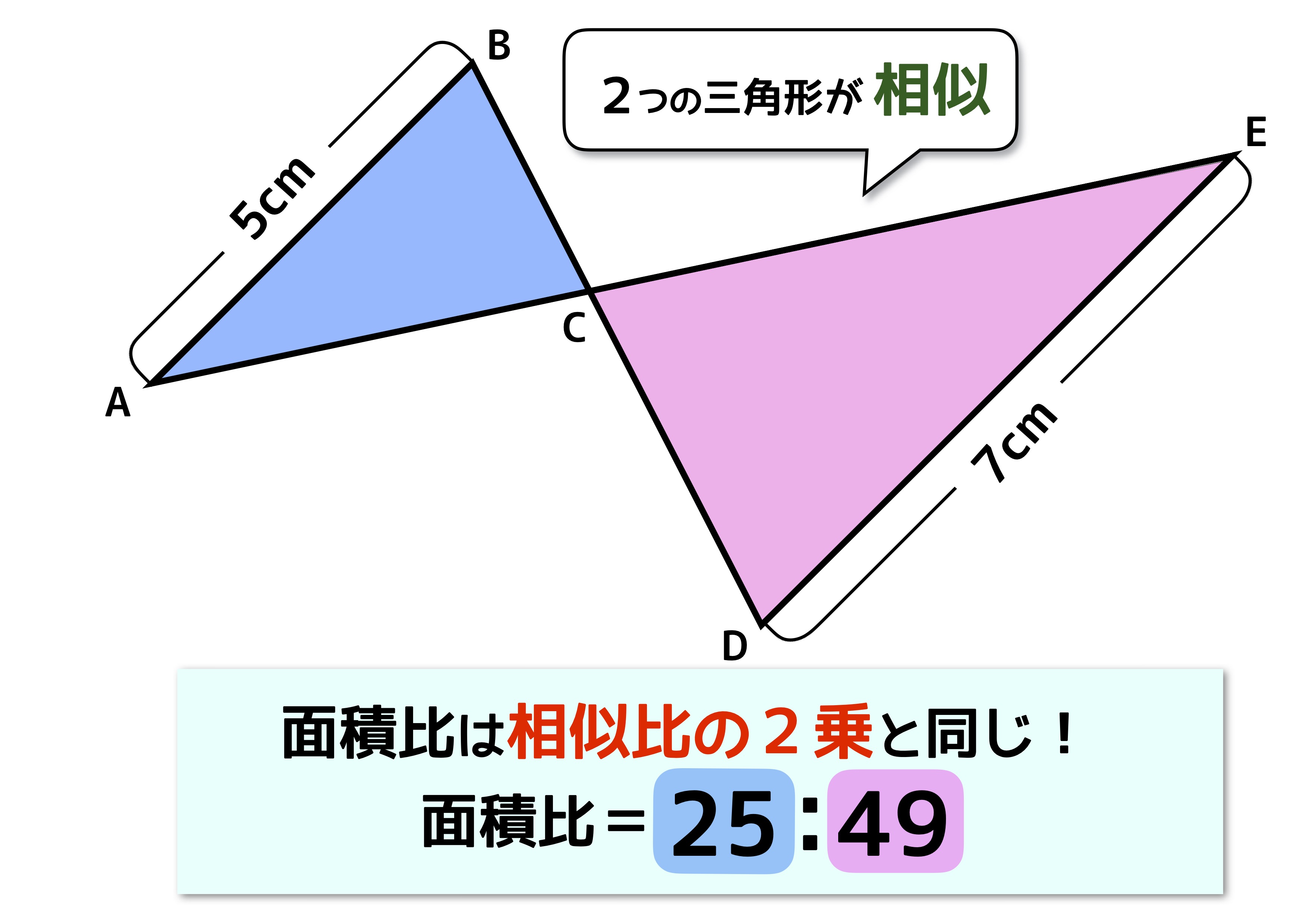



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
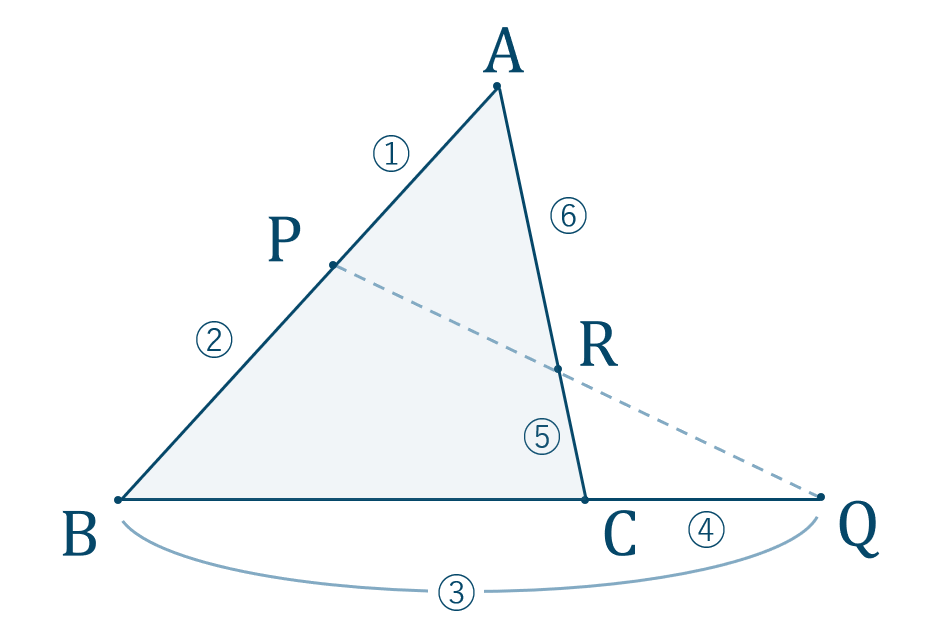



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学




各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア
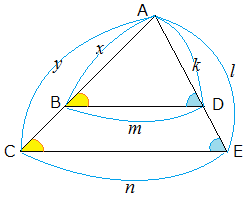



平行線と線分の比




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく



直角三角形の3辺の比について 1 2 3とありますが2と 3の位置 Yahoo 知恵袋




平面図形をマスター 三角形の面積比 応用編その3




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー



3
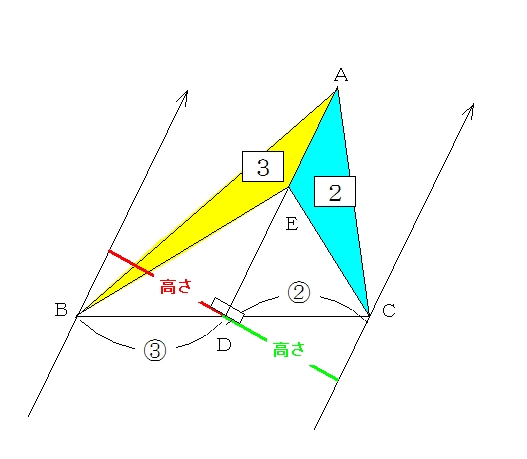



辺の比と面積比




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
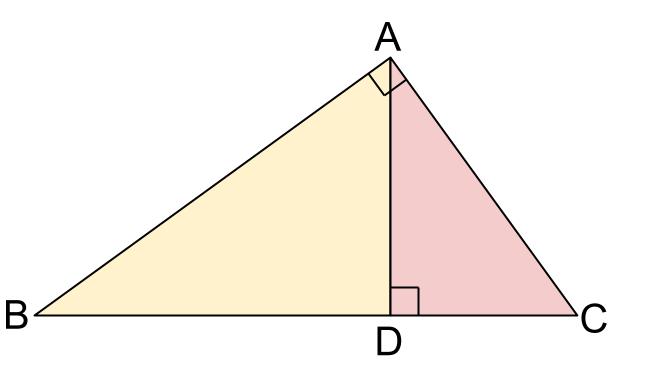



中学数学 直角三角形の相似 中学数学の無料オンライン学習サイトchu Su




平面図形をマスター 三角形の面積比 応用編その3




三平方の定理の証明と使い方



Math 90 30 60 の直角三角形 辺の長さで成り立つこと 働きアリ
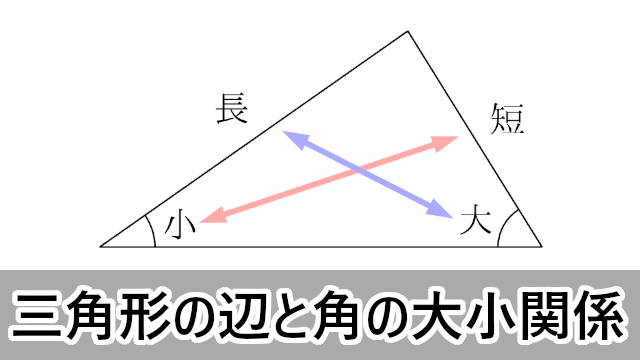



数学ia 三角形の角の大きさと辺の長さの関係 大学入試数学の考え方と解法



3 4 5と1 2 3と3角定規とtvと黄金比と 万象酔歩




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




高校数学 三角形の辺と角の関係 映像授業のtry It トライイット
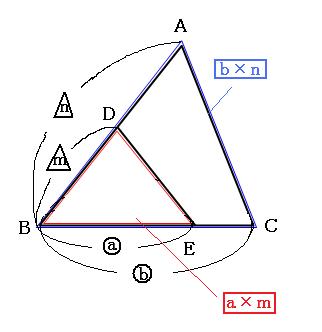



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア



Pr この広告は3ヶ月以上更新がないため表示されています ホームページを更新後24時間以内に表示されなくなります 三平方の定理 三平方の定理とは 三平方の定理 ピタゴラスの定理 定理 任意の直角三角形において 斜辺の長さの自乗は他
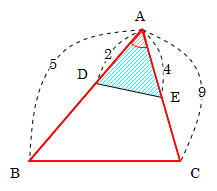



平面図形 辺の比と面積の比 前田昌宏の中学受験が楽しくなる算数塾




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
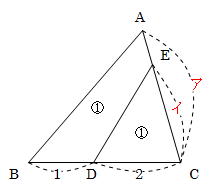



平面図形 辺の比と面積の比 前田昌宏の中学受験が楽しくなる算数塾




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ



M 2 三角形の辺の比を求める 2 Solid Line
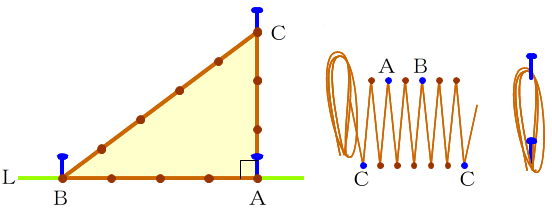



3 4 5の三角形で 本当に直角ができる Note Board




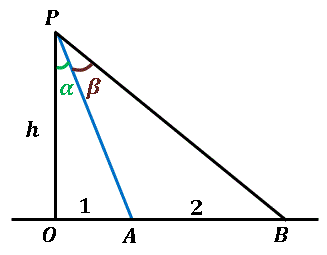
高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月



これまでで最高の三角形 の 底辺 子供のための最高のぬりえ




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



辺の比と面積比



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
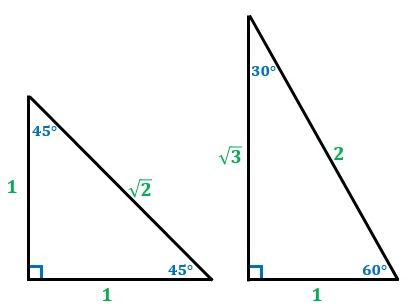



直角三角形の辺の比 東久留米 学習塾 塾長ブログ




中学受験算数 三角形の2辺の比と面積比の問題 Stupedia




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座



0 件のコメント:
コメントを投稿