平行四辺形は2つの 合同 な 三角形 を2つ、対応するひと組の辺を共有し、その両端の頂点が対応と逆順に重なるように並べた図形である。 三角形の面積を 〔底辺〕×〔高さ〕÷2 で表すことができるのは、それが平行四辺形の面積を2等分して求めた結果だなぜ？ 平行四辺形の面積が \( 底辺 \times 高さ \) となるのかを考えてみましょう。 図のように垂線を引き、平行四辺形を「赤い部分」と「青い部分」に分けます。 「青い部分」を切り取って、「赤い部分」の左側へ移動すると、このように平行四辺形は「長方形」に変形できることがわかり1平行四辺形とは？ 平行四辺形は、向かい合う2組の辺が平行な四角形です。 ある四角形について，①2組の対辺がそれぞれ平行であると示せば，平行四辺形であることが証明できるのはわかりますね。 2ポイント ただし，「2組の対辺が平行＝平行四辺形」と覚えるだけでは，平行四辺形の
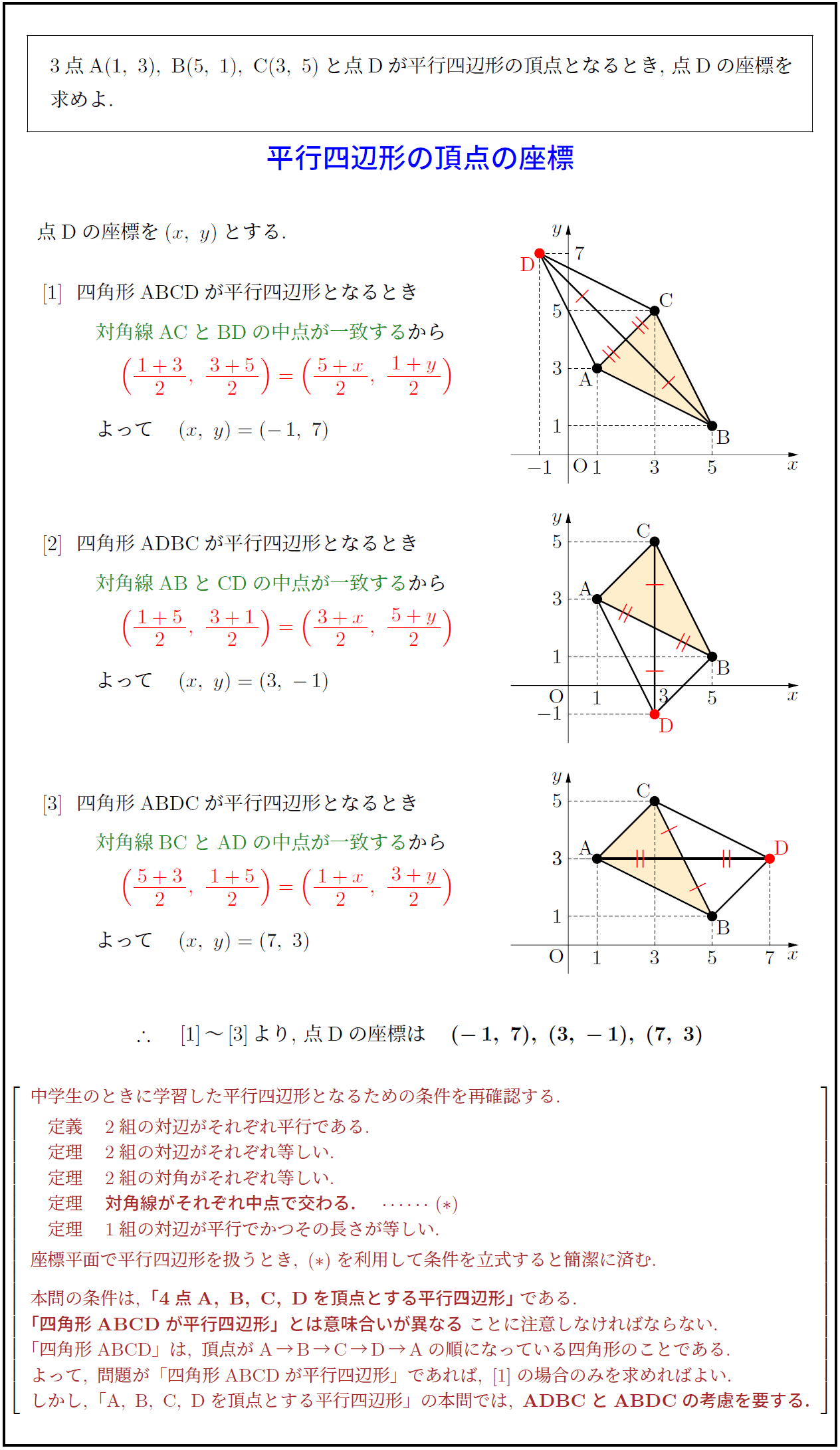
高校数学 平行四辺形の頂点の座標 受験の月
台形を2本の 対角線 で分割すると4つの 三角形 になるが、台形の底辺を辺に持つ2つの三角形の 面積 比 は上底と下底の長さの比の平方に等しい。 台形の面積の求め方が 相変わらず、毎日、毎日、ルワンダの算数の教科書を見ています。 さらっと見ていると日本との違いが分からないのですが、じっくり見ると結構見えてきます。 なかなか面白いです。 今日は、台形の面積の所を見ていました。台形の面積 = (上底 下底) × 高さ ÷ 2
台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
平行線と線分の比について調べることができる。 相似の考え方を活用することができる。 立体の相似の意味と，相似な図形の相似比や面積比，体積比の関係を理解し，それを利用できる。 4 単元の指導平行線と線 分の比 平行線と線 分の比に関 する性質を 見いだし，そ れを証明し， 利用するこ とができる。 三角形の1つの 辺に平行な直線 を引き、そこに できる線分の比 について長さを 調べ、それを証 明する。 平行線と線分の 比についての性質 に関心3 平行線と線分の比 「平行線に直線が交わるとき、その交点の間の比は等しくなる」ことを次のように 証明した。直線l,m,nが平行であるとき、かっこに当てはまる語をうめよう。 点aを通り、直線a′に平行な直線を引き、それと直線m,nの交点をd,eとした。
平行線と線分の比
中2 数学科 「証明とそのしくみ」～証明の方針の立て方を考えよう～ その1 証明の構想や方針を自ら立てることを促すフローチャートを示 したワークシートの工夫 証明指導の導入で、証明の構想や方針を立てたりすることとそれ 問2は，中2から解けますが，中2，中3，高1で解法が異なります。 第回芸術的な難問高校入試 「等脚台形と各々の解法」 出典：オリジナル 範囲：相似，三平方の定理など 難易度：★★★★☆☆ 美しさ：？ 中学2年の三角形合同の証明で, 合同であることが証明した後の合同な図形の対応する 角は等しいから・・・・ を 単に したがって とか よって で記述しても 正解でしょうか。 お願いします。
数学 相似三角形 Hl判定 的证明 哔哩哔哩
专题19菱形、矩形与正方形(60真题60模拟) (共60真题) 一菱形的性质(共15小题) 1(21•南通)菱形的两条对角线的长分别是6和8,则这个菱形的周长是 a24 b c10 d5 分析根据菱形的对角线互相垂直平分的性质,利用对角线的一半,根据勾股定理求出菱形的边长,教材： 初中数学 / 华师大版 / 八年级下册 / 第19章 矩形、菱形与正方形 / 192 菱形 / 1 菱形的性质 标签： 课件 全国 1097 MB 下载5次 5个学币 21jy_正方形如何判定 时间： 来源：养娃家 有一组邻边相等，并且有一个角是直角的平行四边形称为正方形，又称正四边形，它是特殊的平行四边形之一，具有矩形和菱形的全部特性。
三角形菱形正方形金边大理石花纹立体
合同式の証明や問題の解き方を解説！大学受験で使いこなそう！ 数学 勉強法;中学数学 平行と合同の内容 z 平行線と角 z 対頂角 z 同位角と錯角 z 三角形の角 z多角形の角 z図形の合同 z 三角形の合同条件 z 仮定と結論 z 証明 ＊「ページ表示」を「見開き」でご覧いただきますと、問題とその 答えが見やすくなります。合同証明応用(直線と内角の和) 合同証明応用(角の引き算) 二等辺三角形の角 平行四辺形証明 折り返し 平行線と面積 等積変形1 等積変形2 三角形・四角形 練習問題
中学２年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
